Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-29T19:45:28.134Z Has data issue: false hasContentIssue false
  • English
  • Français

Poincaré and Friedrichs inequalities in abstract Sobolev spaces II

Published online by Cambridge University Press:  24 October 2008

D. E. Edmunds ,
B. Opic  and
J. Rákosník
D. E. Edmunds
Affiliation:
Mathematics Division, University of Sussex
B. Opic
Affiliation:
Mathematical Institute, Czechoslovak Academy of Sciences, Prague
J. Rákosník
Affiliation:
Mathematical Institute, Czechoslovak Academy of Sciences, Prague
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is a continuation of [4]; its aim is to extend the results of that paper to include abstract Sobolev spaces of higher order and even anisotropic spaces. Let Ω be a domain in ℝN, let X = X(Ω) and Y = Y(Ω) be Banach function spaces in the sense of Luxemburg (see [4] for details), and let W(X, Y) be the abstract Sobolev space consisting of all f ∈ X such that for each i ∈ {l, …, N} the distributional derivative 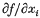belongs to Y; equipped with the norm

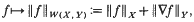
W(X, Y) is a Banach space. Given any weight function w on Ω, the triple [w, X, Y] is said to support the Poincaré inequality on Ω. if there is a positive constant K such that for all u ∈ W(X, Y)

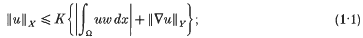
the pair [X, Y] is said to support the Friedrichs inequality if there is a positive constant K such that for all u ∈ W0(X, Y) (the closure of 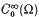in W(X, Y))

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 115 , Issue 1 , January 1994 , pp. 159 - 173
Copyright
Copyright © Cambridge Philosophical Society 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Besov, O. V., Il'in, V. P. and Nikol'skii, S. M.. Integral Representations of functions and imbedding theorems. Vol. II. (Winston, Washington, 1979).Google Scholar
[2]Edmunds, D. E. and Evans, W. D.. Spectral theory and differential operators (Clarendon Press, 1987).Google Scholar
[3]Edmunds, D. E. and Opic, B.. Weighted Poincaré and Friedrichs inequalities. J. London Math. Soc. (2) 47 (1993), 79–93.Google Scholar
[4]Edmunds, D. E., Opic, B. and Pick, L.. Poincaré and Friedrichs inequalities in abstract Sobolev spaces. Math. Proc. Cambridge Phil. Soc. 113 (1993), 355–379.Google Scholar
[5]Goldberg, S.. Unbounded linear operators (McGraw-Hill, 1966).Google Scholar
[6]Kufner, A., John, O. and Fučík, S.. Function spaces (Academia, Prague and Noordhoff International Publishing, 1977).Google Scholar
[7]Nečas, J.. Les méthodes directes en théorie des équations elliptiques (Academia, Prague and Masson, 1967).Google Scholar
[8]Opic, B. and Rákosník, J.. Estimates for mixed derivatives of functions from anisotropic Sobolev-Slobodeckij spaces with weights. Quart. J. Math. Oxford (2) 42 (1991), 347–363.Google Scholar
[9]Ziemer, W.. Weakly differentiable functions (Springer-Verlag, 1989).CrossRefGoogle Scholar