Hostname: page-component-7479d7b7d-c9gpj Total loading time: 0 Render date: 2024-07-08T10:10:42.759Z Has data issue: false hasContentIssue false
  • English
  • Français

Permutation endomorphisms and refinement of a theorem of Birkhoff

Published online by Cambridge University Press:  24 October 2008

H. K. Farahat  and
L. Mirsky
H. K. Farahat
Affiliation:
The UniversitySheffield
Get access Rights & Permissions [Opens in a new window]

Extract

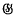Let be a free additive abelian group, and let 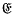be a basis of 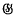, so that every element of 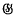can be expressed in a unique way as a (finite) linear combination with integral coefficients of elements of 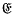. We shall be concerned with the ring of endomorphisms of 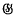, the sum and product of the endomorphisms φ, χ being defined, in the usual manner, by the equations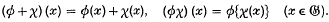

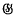A permutation of a set will be called restricted if it moves only a finite number of elements. We call an endomorphism of a permutation endomorphism if it induces a restricted permutation of the basis .

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 56 , Issue 4 , October 1960 , pp. 322 - 328
Copyright
Copyright © Cambridge Philosophical Society 1960

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Berge, C.Théorie des graphes et ses applications (Paris, 1958).Google Scholar
(2)Birkhoff, G.Tres observaciones sobre el algebra lineal. Univ. Nac. Tucumán, Rev. Ser. A, 5 (1946), 147–50.Google Scholar
(3)Carathéodory, C.Über den Variabilitätsbereich der Fourierschen Konstanten von positiven harmonischen Funktionen. R. C. Circ. mat. Palermo, 32 (1911), 193–217.Google Scholar
Reprinted in Gesammelte mathematische Schriften (M–unchen, 1954–1957), vol. III, 78–110.Google Scholar
(4)Dulmage, L. and Halperin, I.On a theorem of Frobenius—König and J. von Neumann's game of hide and seek. Trans. Roy. Soc. Canada, Section III (3), 49 (1955), 23–9.Google Scholar
(5)Eggleston, H. G.Convexity (Cambridge, 1958).Google Scholar
(6)Farahat, H. K.The symmetric group as metric space. J. London Math. Soc., 35 (1960), 215–20.Google Scholar
(7)Hoffman, A. J. and Wielandt, H. W.The variation of the spectrum of a normal matrix. Duke Math. J. 20 (1953), 37–40.Google Scholar
(8)Marcus, M. and Newman, M.On the minimum of the permanent of a doubly stochastic matrix. Duke Math. J. 26 (1959), 61–72.CrossRefGoogle Scholar
(9)Mirsky, L.Proofs of two theorems on doubly-stochastic matrices. Proc. Amer. Math. Soc. 9 (1958), 371–4.Google Scholar
(10)Neumann, J. Von. A certain zero-sum two-person game equivalent to the optimal assignment problem. Contributions to the theory of games, vol. II (Princeton, 1953), 5–12.Google Scholar