Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-30T20:37:40.374Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic groups generated by finite amalgams

Published online by Cambridge University Press:  24 October 2008

Kenneth K. Hickin ,
Richard E. Phillips  and
J. M. Plotkin
Kenneth K. Hickin
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824
Richard E. Phillips
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824
J. M. Plotkin
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824
Get access Rights & Permissions [Opens in a new window]

Extract

The following embedding theorem was proved in the paper (7). Let Π be a set of primes and P, H and K periodic Π-groups satisfying

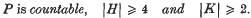
Then there is a period Π-group J generated by isomorphic copies of H and K such that P ≤ J.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 87 , Issue 2 , March 1980 , pp. 189 - 197
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Adyan, S. I.On the simplicity of periodic products of groups. Dokl. Akad. Nauk USSR, 241 (1978) ( = Soviet Math. Dokl. 19 (1978), 910–913).Google Scholar
(2)Adyan, S. I.The Burnside problem and identities in groups (New York, Springer-Verlag, 1978).Google Scholar
(3)Day, G. W.Superatomic Boolean algebras. Pacific J. Math. 23 (1967), 479–489.Google Scholar
(4)Hall, P.On the embedding of a group in a join of given groups. J. Austral. Math. Soc. 17 (1974), 434–495.Google Scholar
(5)Hickin, K. K.An embedding theorem for periodic groups. J. London Math. Soc. (2) 14 (1976), 63–64.CrossRefGoogle Scholar
(6)Hickin, K. K. and Phillips, R. E.Non-isomorphic Burnside groups of exponent p 2. Canad. J. Math. 30 (1978), 180–189.Google Scholar
(7)Hickin, K. K. and Phillips, R. E.Joins of periodic groups. Proc. London Math. Soc. (3) 39 (1979), 176–192.CrossRefGoogle Scholar
(8)Jeanes, S. Counting the periodic subgroups generated by two finite groups. (To appear.)Google Scholar
(9)Karass, A. and Solitar, D.The subgroups of a free product of two groups with an amalgamated subgroup. Trans. Amer. Math. Soc. 150 (1970), 227–255.Google Scholar
(10)Mostowski, A. and Tarski, A.Boolesche Ringe mit geordneter Basis. Fund. Math. 32 (1939), 69–86.Google Scholar
(11)Novikov, P. S. and Adyan, S. I.Infinite periodic groups, Izv. Akad. Nauk USSR Ser. Mat. 32 (1968), 212–244; 251–524; 709–731 (= Math. USSR Izv. 2 (1968), 209–236, 241–479, 665–685).Google Scholar
(12)Phillips, R. E.Embedding methods for periodic groups. Proc. London Math. Soc. (3) 35 (1977), 238–256.Google Scholar
(13)Plotkin, B.I Generalized solvable and generalized nilpotent groups Uspehi. Mat. Nauk (N.S.) 13 (1958), 89–172 ( = Amer. Math. Soc. Transl. (2) 17, 29–116).Google Scholar