Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T14:13:07.584Z Has data issue: false hasContentIssue false
  • English
  • Français

A pathological case of the C1 conjecture in mixed characteristic

Published online by Cambridge University Press:  05 April 2018

INDER KAUR
INDER KAUR*
Affiliation:
Instituto Nacional de Matemática Pura e Aplicada, Estr. Dona Castorina, 110 - Jardim Botânico, Rio de Janeiro - RJ, 22460-320, Brazil. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be a field of characteristic 0. Fix integers r, d coprime with r ⩾ 2. Let XK be a smooth, projective, geometrically connected curve of genus g ⩾ 2 defined over K. Assume there exists a line bundle 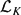${\cal L}_K$ on XK of degree d. In this paper we prove the existence of a stable locally free sheaf on XK with rank r and determinant 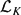${\cal L}_K$. This trivially proves the C1 conjecture in mixed characteristic for the moduli space of stable locally free sheaves of fixed rank and determinant over a smooth, projective curve.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 167 , Issue 1 , July 2019 , pp. 61 - 64
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bhosle, U. and Biswas, I.. Stable real algebraic vector bundles over a Klein bottle. Trans. Amer. Math. Soc. 360 (9) (2008), 4569–4595.Google Scholar
[2] Colliot-Thélene, J. L. Variétés presque rationnelles, leurs points rationnels et leurs dégénére-scences. In Arithmetic Geometry (Springer, 2010), pages 1–44.Google Scholar
[3] Kaur, I. Smoothness of moduli space of stable torsionfree sheaves with fixed determinant in mixed characteristic. In Analytic and Algebraic Geometry (Springer, 2017), pages 173–186.Google Scholar
[4] Lang, S. On quasi algebraic closure. Annals of Math. 55 (1952), 373–390.Google Scholar
[5] Langer, A. Semistable sheaves in positive characteristic. Annals of Math. 159 (2004), 251–276.10.4007/annals.2004.159.251Google Scholar
[6] Le Potier, J. Lectures on Vector Bundles, volume 54 (Cambridge University Press, 1997).Google Scholar
[7] Mestrano, N. Conjecture de franchetta forte. Invent. Math. 87 (2) (1987), 365–376.Google Scholar
[8] Seshadri, C.S. Fibres vectoriels sur les courbes algebriques. vol. 14023. Astérisque 96 (Paris, 1982).Google Scholar