A paranormed space X = (X, g) is a topological linear space in which the topology is given by paranorm g—a real subadditive function on X such that g(θ) = 0, g(x) = g(−x) and such that multiplication is continuous. In the above, θ is the zero in the complex linear space X and continuity of multiplication means that λn → λ, xn → x(i.e. g(xn − x) → 0) imply λnxn → λx, for scalars λ and vectors x. We shall use the term semimetric function to describe a real subadditive function g on X such that g(θ) = 0, g(x) = g(−x). Two familiar paranormed sequence spaces, which have been extensively studied (3), are l(p) and m(p). 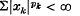For a given sequence p = (gk) of strictly positive numbers, l;(p) is the set of all complex sequences x = (xk) such that and m(p) is the set of x such that sup 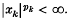Throughout, sums and suprema without limits are taken from 1 to ∞. Simons (3) considered only the case in which 0 < pk ≤ 1 so that natural paranorms would seem to be 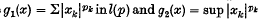in m(p). In fact Simons showed that g1 was a paranorm for l(p), but that g2 did not satisfy the continuity of multiplication axiom.