Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T07:38:14.896Z Has data issue: false hasContentIssue false
  • English
  • Français

Open decompositions on ordered convex spaces

Published online by Cambridge University Press:  24 October 2008

Yau-Chuen Wong
Yau-Chuen Wong
Affiliation:
United College, The Chinese University of Hong Kong
Get access Rights & Permissions [Opens in a new window]

Extract

Let (E, 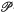) be a topological vector space with a positive cone C. Jameson (3) says that C given an open decomposition on E if V ∩ C − V ∩ C is a 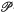-neighbourhood of 0 whenever V is a 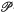-neighbourhood of 0. The concept of open decompositions plays an important rôle in the theory of ordered topological vector spaces; see (3). It is clear that C is generating if C gives an open decomposition on E; the converse is true for Banach spaces with a closed cone, by Andô's theorem (cf. (1) or (9)). Therefore the following question arises naturally:

(Q 1) Let (E, 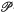) be a locally convex space with a positive cone C. What condition on 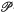is necessary and sufficient for the cone C to give an open decomposition on E?

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 74 , Issue 1 , July 1973 , pp. 49 - 59
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Andô, T.On fundamental properties of a Banach space with a cone. Pacific J. Math. 12 (1962), 1163–1169.Google Scholar
(2)Baker, J. W.Continuity in ordered spaces. Math. Z. 104 (1968), 231–246.CrossRefGoogle Scholar
(3)Jameson, G. J. O.Ordered linear spaces Lecture Notes in Math. (104), (Springer-Verlag, Berlin, 1970).CrossRefGoogle Scholar
(4)Kist, J.Locally o-convex space. Duke Math. J. 25 (1958), 569–582.CrossRefGoogle Scholar
(5)Nachbin, L.Topology and order (Van Nostrand, Princeton, 1965).Google Scholar
(6)Namioka, I.Partially ordered linear spaces. Memoirs American Math. Soc. 24 (1957).Google Scholar
(7)Ng, K.-F.Solid sets in ordered topological vector spaces. Proc. London Math. Soc. (3), 22 (1971), 106–120.Google Scholar
(8)Peressini, A. L.Ordered topological vector spaces (Harper and Row, New York, 1967).Google Scholar
(9)Schaefer, H. H.Topological vector spaces (Macmillan, New York, 1966).Google Scholar
(10)Warner, S.Bornological structures. Illinois J. Math. 4 (1960), 231–245.CrossRefGoogle Scholar
(11)Wong, Yau-ChuenLocally o-convex Riesz spaces. Proc. London Math. Soc. (3) 19 (1969), 289–309.CrossRefGoogle Scholar
(12)Wong, Yau-ChuenOrder-infrabarrelled Riesz spaces. Math. Ann. 183 (1969), 17–32.Google Scholar
(13)Wong, Yau-Chuen.The order-bound topology on Riesz spaces. Proc. Cambridge Philos. Soc. 67 (1970), 587–593.CrossRefGoogle Scholar