Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T13:12:00.893Z Has data issue: false hasContentIssue false
  • English
  • Français

On two theorems of S. Verblunsky

Published online by Cambridge University Press:  24 October 2008

Hubert Delange
Hubert Delange
Affiliation:
Faculté des SciencesUniversité de ClermontClermont-FerrandFrance
Get access Rights & Permissions [Opens in a new window]

Extract

In connexion with moment problems, S. Verblunsky proved the following two theorems:

Theorem I. (a) If f(x) is integrable in (−∞, +∞) and satisfies 0 ≤f(x) ≤ 1, then there exists a function σ(x), bounded and non-decreasing in (−∞, +∞), such that, for ζ = ξ + iη and η ≠ 0,

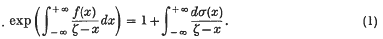
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 1 , January 1950 , pp. 57 - 66
Copyright
Copyright © Cambridge Philosophical Society 1950

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* ‘Two moment problems for bounded functions’, Proc. Cambridge Phil. Soc. 42 (1946), 189–96.CrossRefGoogle Scholar

† ‘On the initial moments of a bounded function’, Proc. Cambridge Phil. Soc. 43 (1947), 275–9.CrossRefGoogle Scholar

* We omit the trivial case when f(x) = 0 almost everywhere.

† Notice that so that these inequalities define non-overlapping intervals.

* We omit the trivial case when σ(x) is constant.

* A very similar lemma was proved by Stieltjes, , Ann. Fac. Sci. Toulouse (1), 8 (1894), J72–J75.CrossRefGoogle Scholar

* A > 0 if a 1 > 0 and A = 0 if a 1 = 0.

* For instance, we may take