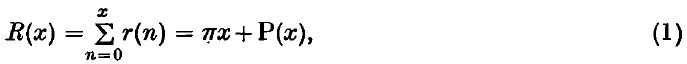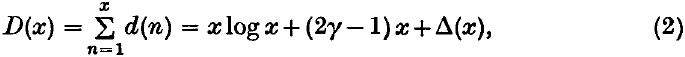Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pennington, W. B.
1951.
On the order of magnitude of Ramanujan's arithmetical function τ(n).
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 47,
Issue. 4,
p.
668.
Chandrasekharan, K.
and
Narasimhan, Raghavan
1961.
On Hecke’s functional equation.
Bulletin of the American Mathematical Society,
Vol. 67,
Issue. 2,
p.
182.
Gangadharan, K. S.
and
Ingham, A. E.
1961.
Two classical lattice point problems.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 57,
Issue. 4,
p.
699.
Joris, Henri
1972.
Ω-Sätze für zwei arithmetische Funktionen.
Commentarii Mathematici Helvetici,
Vol. 47,
Issue. 1,
p.
220.
Schierwagen, Andreas
1976.
Über ein Teilerproblem.
Mathematische Nachrichten,
Vol. 72,
Issue. 1,
p.
151.
Nowak, Werner Georg
1985.
An Ω-estimate for the lattice rest of a convex planar domain.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 100,
Issue. 3-4,
p.
295.
Estrada, Ricard
1992.
The asymptotic expansion of certain series considered by ramanujan.
Applicable Analysis,
Vol. 43,
Issue. 3-4,
p.
191.
Ivić, Aleksander
and
Matsumoto, Kohji
1996.
On the error term in the mean square formula for the Riemann zeta-function in the critical strip.
Monatshefte für Mathematik,
Vol. 121,
Issue. 3,
p.
213.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
365.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
13.
Chattopadhyay, Jaitra
and
Darbar, Pranendu
2019.
Mean values and moments of arithmetic functions over number fields.
Research in Number Theory,
Vol. 5,
Issue. 3,