Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T13:52:16.830Z Has data issue: false hasContentIssue false
  • English
  • Français

On ‘translated quasi-Cesàro’ summability

Published online by Cambridge University Press:  24 October 2008

B. Kuttner
B. Kuttner
Affiliation:
University of Birmingham
Get access Rights & Permissions [Opens in a new window]

Extract

Corresponding to a fixed sequence {μn}, the Hausdorff method of summability (H, μn) is defined by the sequence-to-sequence transformation†

where we write

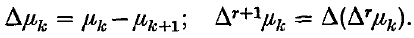
The quasi-Hausdorff method (H*, μn) is defined by the transformation

thus the matrix of the (H*, μn) transformation is the transpose of that of the (H*, μn) transformation. A method introduced by Ramanujan (9), which we will call‡ (S,μn) is given by the transformation

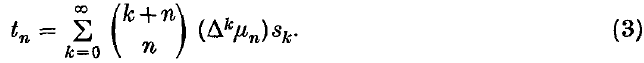
Thus the elements of row n of the matrix of the (S, μn) transformation are those of the corresponding row of the (H*, μn) transformation moved n places to the left.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 4 , October 1966 , pp. 705 - 712
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Gergen, J. J.Summability of double Fourier series. Duke Math. J. 3 (1937), 133–148. (Part I, 133–137.)CrossRefGoogle Scholar
(2)Hardy, G. H.Divergent series (Oxford, 1949).Google Scholar
(3)Hobson, E. W.Functions of a real variable (vol. II) (Cambridge, 1926).Google Scholar
(4)Ishiguro, K.On the summability methods of divergent series. Acad. Roy. Belg. Cl. Sci. Mém. Coll. in-8° 35 (1965), 1–43.Google Scholar
(5)Jurkat, W.Über Rieszche Mittel und verwandte Klassen von Matrixtransformationen. Math. Z. 37 (1953), 353–394.Google Scholar
(6)Kuttner, B.Some remarks on quasi-Hausdorff transformations. Quart. J. Math. Oxford Ser. (2), 8 (1957), 272–278.CrossRefGoogle Scholar
(7)Kuttner, B.Some theorems on the Cesàro limit of a function. J. London Math. Soc. 33 (1958), 107–118.CrossRefGoogle Scholar
(8)Kuttner, B.On ‘quasi-Cesàro’ summability. J. Indian Math. Soc. 24 (1960), 319–341.Google Scholar
(9)Ramanujan, M. S.On Hausdorff and quasi-Hausdorff methods of summability. Quart. J. Math. Oxford Ser. (2), 8 (1957), 197–213.CrossRefGoogle Scholar
(10)Riesz, M.Une méthode de sommation équivalente a la méthode des moyennes arithmétiques. C.R. Acad. Sci. Paris 152 (1911), 1651–1654.Google Scholar
(11)White, A. J.On ‘quasi-Cesàro’ summability. Quart. J. Math. Oxford Ser. (2), 12 (1961), 81–99.CrossRefGoogle Scholar