Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T14:17:10.875Z Has data issue: false hasContentIssue false
  • English
  • Français

On the transfer in the homology of symmetric groups

Published online by Cambridge University Press:  24 October 2008

Daniel S. Kahn  and
Stewart B. Priddy
Daniel S. Kahn
Affiliation:
Northwestern University, Evanston, Illinois, U.S.A.
Stewart B. Priddy
Affiliation:
Northwestern University, Evanston, Illinois, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

The transfer has long been a fundamental tool in the study of group cohomology. In recent years, symmetric groups and a geometric version of the transfer have begun to play an important role in stable homotopy theory (2, 5). Thus, motivated by geometric considerations, we have been led to investigate the transfer homomorphism

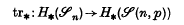
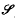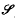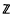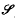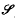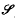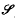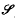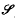in group homology, where n is the nth symmetric group, (n, p) is a p-Sylow sub-group and simple coefficients are taken in /p (the integers modulo a prime p). In this paper, we obtain an explicit characterization (Theorem 3·8) of this homomorphism. Roughly speaking, elements in H*(n) are expressible in terms of the wreath product k ∫ l → n (n = kl) and the ordinary product k × n−k→ 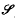n. We show that tr* preserves the form of these elements.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 83 , Issue 1 , January 1978 , pp. 91 - 101
Copyright
Copyright © Cambridge Philosophical Society 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1) Adem, J. The relations on Steenrod powers of cohomology classes. Algebraic geometry and topology, A symposium in honor of S. Lefschetz (Princeton, 1957).Google Scholar
(2) Becker, J. C. and Gottlieb, D. H. The transfer map and fibre bundles. Topology 14 (1975), 1–12.CrossRefGoogle Scholar
(3) Cartan, H. and Eilenberg, S. Homological algebra (Princeton N.J.: Princeton University Press, 1956).Google Scholar
(4) Dyer, E. and Lashof, R. K. Homology of iterated loop spaces. Amer. J. Math. 84 (1962), 357–88CrossRefGoogle Scholar
(5) Kahn, D. S. and Priddy, S. B. Applications of the transfer to stable homotopy theory. Bull. Amer. Math. Soc. 78 (1972), 981–987.CrossRefGoogle Scholar
(6) Kahn, D. S. and Priddy, S. B. Transfer, symmetric groups and stable homotopy theory; algebraic K-theory 1. Lecture Note B in Mathematics, no. 341 (1973), 244–255.Google Scholar
(7) May, J. P. A general approach to Steenrod operations. Lecture Notes in Mathematics, no. 168 (1970).CrossRefGoogle Scholar
(8) Nakaoka, M. Homology of the infinite symmetric group. Ann. of Math. (2) 73 (1961), 229–257.CrossRefGoogle Scholar
(9) Nakaoka, M. Decomposition theorem for homology groups of symmetric groups. Ann. of Math. (2) 71 (1961), 16–42.Google Scholar
(10) Priddy, S. B. Homotopy splittings involving G and G/O. (To appear.)Google Scholar
(11) Wielandt, H. Finite permutation groups (New York: Academic Press, 1964).Google Scholar