Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kelly-Lyth, D.
and
McCrudden, M.
1996.
Supports of gauss measures on semisimple lie groups.
Mathematische Zeitschrift,
Vol. 221,
Issue. 1,
p.
633.
Hazod, Wilfried
and
Siebert, Eberhard
2001.
Stable Probability Measures on Euclidean Spaces and on Locally Compact Groups.
p.
181.
Bingham, N.H.
and
Ostaszewski, A.J.
2019.
Beyond Haar and Cameron-Martin: The Steinhaus support.
Topology and its Applications,
Vol. 260,
Issue. ,
p.
23.


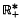 (under addition) into
(under addition) into