Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-29T22:31:08.383Z Has data issue: false hasContentIssue false
  • English
  • Français

On the structure of simplicial categories associated to quasi-categories

Published online by Cambridge University Press:  11 March 2011

EMILY RIEHL
EMILY RIEHL*
Affiliation:
Department of Mathematics, University of Chicago, 5734 S. University Ave., Chicago, IL 60637, USA e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The homotopy coherent nerve from simplicial categories to simplicial sets and its left adjoint 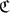are important to the study of (∞, 1)-categories because they provide a means for comparing two models of their respective homotopy theories, giving a Quillen equivalence between the model structures for quasi-categories and simplicial categories. The functor 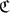also gives a cofibrant replacement for ordinary categories, regarded as trivial simplicial categories. However, the hom-spaces of the simplicial category 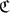X arising from a quasi-category X are not well understood. We show that when X is a quasi-category, all Λ21 horns in the hom-spaces of its simplicial category can be filled. We prove, unexpectedly, that for any simplicial set X, the hom-spaces of 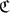X are 3-coskeletal. We characterize the quasi-categories whose simplicial categories are locally quasi, finding explicit examples of 3-dimensional horns that cannot be filled in all other cases. Finally, we show that when X is the nerve of an ordinary category, 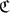X is isomorphic to the simplicial category obtained from the standard free simplicial resolution, showing that the two known cofibrant “simplicial thickenings” of ordinary categories coincide, and furthermore its hom-spaces are 2-coskeletal.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 150 , Issue 3 , May 2011 , pp. 489 - 504
Copyright
Copyright © Cambridge Philosophical Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bergner, J.A model category structure on the category of simplicial categories. Trans. Amer. Math. Soc. 359 (2007), 2043–2058.CrossRefGoogle Scholar
[2]Bergner, J. A survey of (∞, 1)-categories. Towards higher categories. IMA Vol. Math. Appl. 152 (Springer, 2010), pp. 69–83.CrossRefGoogle Scholar
[3]Cordier, J.-M.Sur la notion de diagramme homotopiquement cohérent. Cah. Top. Géom. Difféc. 1 XXIII (1982), 93–112.Google Scholar
[4]Cordier, J.-M. and Porter, T.Vogts theorem on categories of homotopy coherent diagrams. Math. Proc. Cambr. Phil. Soc. 100 (1986), 65–90.CrossRefGoogle Scholar
[5]Day, B. On closed categories of functors. Reports of the Midwest Category Seminar IV. Lecture Notes in Math. vol. 137 (Springer 1970), pp. 1–38.Google Scholar
[6]Dugger, D. and Spivak, D.Rigidification of quasi–categories. Algebr. Geom. Topol. 11 (2011), 225–261.CrossRefGoogle Scholar
[7]Duskin, J.Simplicial matrices and the nerves of weak n-categories I: Nerves of bicategories. CT2000 Conference (Como). Theory Appl. Categ. (10) 9 (2001/2002), 198–308.Google Scholar
[8]Duskin, J.Simplicial methods and the interpretation of “triple” cohomology. Mem. Amer. Math. Soc. 3 (2), no. 16 (1975).Google Scholar
[9]Dwyer, W. and Kan, D.Simplicial localizations of categories. J. Pure Appl. Algebra 17 (1980), 267–284.CrossRefGoogle Scholar
[10]Gabriel, P. and Zisman, M.Calculus of fractions and homotopy theory. Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 35 (Springer-Verlag, 1967).CrossRefGoogle Scholar
[11]Goerss, P. and Jardine, J. Simplicial homotopy theory. Progr. Math. 174 (Birkhauser Verlag, 1999).Google Scholar
[12]Hovey, M. Model categories. Math. Surv. Monogr. vol. 63 (American Mathematical Society, 1999).Google Scholar
[13]Joyal, A.Quasi-categories and Kan complexes. J. Pure Appl. Algebra 175 (2002), 207–222.CrossRefGoogle Scholar
[14]Joyal, A. The theory of quasi-categories I. In progress (2008).Google Scholar
[15]Lurie, J.Higher topos theory. Ann. of Math. Stud. 170 (2009).Google Scholar