Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T19:42:35.130Z Has data issue: false hasContentIssue false
  • English
  • Français

On the size of the maximum of incomplete Kloosterman sums

Part of: Limit theorems Exponential sums and character sums (Co)homology theory Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  15 April 2021

DANTE BONOLIS
DANTE BONOLIS*
Affiliation:
IST Austria, Am Campus 1, 3400 Klosterneuburg, Austria. e-mails: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 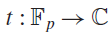$t:{\mathbb F_p} \to C$ be a complex valued function on 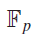${\mathbb F_p}$. A classical problem in analytic number theory is bounding the maximum

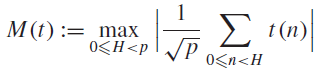$$M(t): = \mathop {\max }\limits_{0 \le H < p} \left| {{1 \over {\sqrt p }}\sum\limits_{0 \le n < H} {t(n)} } \right|$$
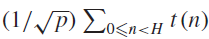of the absolute value of the incomplete sums $(1/\sqrt p )\sum\nolimits_{0 \le n < H} {t(n)} $. In this very general context one of the most important results is the Pólya–Vinogradov bound
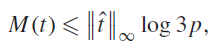$$M(t) \le {\left\| {\hat t} \right\|_\infty }\log 3p,$$
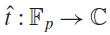where $\hat t:{\mathbb F_p} \to \mathbb C$ is the normalized Fourier transform of t. In this paper we provide a lower bound for certain incomplete Kloosterman sums, namely we prove that for any 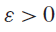$\varepsilon > 0$ there exists a large subset of 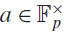$a \in \mathbb F_p^ \times $ such that for 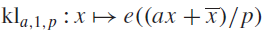$${\rm{k}}{1_{a,1,p}}:x \mapsto e((ax + \bar x)/p)$$ we have
$$M({\rm{k}}{1_{a,1,p}}) \ge \left( {{{1 - \varepsilon } \over {\sqrt 2 \pi }} + o(1)} \right)\log \log p,$$
as $p \to \infty $. Finally, we prove a result on the growth of the moments of 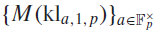${\{ M({\rm{k}}{1_{a,1,p}})\} _{a \in \mathbb F_p^ \times }}$.

MSC classification

Primary: 11L03: Trigonometric and exponential sums, general 11T23: Exponential sums
Secondary: 14F20: Étale and other Grothendieck topologies and (co)homologies 60F10: Large deviations
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 3 , May 2022 , pp. 563 - 590
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

References

Autissier, P., Bonolis, D. and Lamzouri, Y.. The distribution of the maximum of partial sums of Kloosterman sums and other trace functions. Submitted, 45 pages. arXiv:1909.03266.Google Scholar
Bober, J.W. and Goldmakher, L.. The distribution of the maximum of character sums. Mathematika 59(2) (2013), 427–442.CrossRefGoogle Scholar
Barton, J. T., Montgomery, H.L. and Vaaler, J. D.. Note on a Diophantine inequality in several variables. Proc. Amer. Math. Soc. 129(2) (2001), 337–345.CrossRefGoogle Scholar
Deligne, P.. Cohomologie étale (SGA) . Lecture Notes in Math. Vol. 569 (Springer-Verlag, 1977).Google Scholar
Deligne, P.. La conjecture de Weil. II. Inst. Hautes Études Sci. Publ. Math. (52) (1980), 137–252.CrossRefGoogle Scholar
Fouvry, É., Kowalski, E. and Michel, P.. Trace functions over finite fields and their applications. Colloquia. Ed. Norm. vol. 5 (Pisa, 2014).Google Scholar
Fouvry, É., Kowalski, E. and Michel, P.. Algebraic twists of modular forms and Hecke orbits. Geom. Funct. Anal. 25(2) (2015), 580–657.CrossRefGoogle Scholar
Fouvry, É., Kowalski, E. and Michel, P.. A study in sums of products. Philos. Trans. Roy. Soc. A 373(2040) (2015), 26.Google Scholar
Fouvry, É., Kowalski, E., Michel, P., Raju, C. S, Rivat, J. and Soundararajan, K.. On short sums of trace functions. Ann. Inst. Fourier (Grenoble) 67(1) (2019), 423–449.CrossRefGoogle Scholar
Fouvry, É., Kowalski, E. and Michel, P.. On the conductor of cohomological transforms. Submitted, arXiv:1310.3603.Google Scholar
Fouvry, É., Kowalski, E., Michel, P. and Sawin, W.. Lectures on applied l-adic cohomology. Contemp. Math. (2019).Google Scholar
Goldmakher, L. and Lamzouri, Y.. Lower bounds on odd order character sums. Int. Math. Res. Not. IMRN (21) (2012), 5006–5013.CrossRefGoogle Scholar
Goldmakher, L. and Lamzouri, Y.. Large even order character sums. Proc. Amer. Math. Soc. 142(8) (2014), 2609–2614.CrossRefGoogle Scholar
Granville, A. and Soundararajan, K.. Large character sums: pretentious characters and the Pólya-Vinogradov theorem. J. Amer. Math. Soc. 20(2) (2007), 357–384.CrossRefGoogle Scholar
Hooley, C.. On the greatest prime factor of a cubic polynomial. J. Reine Angew. Math. 303/304 (1978), 21–50.Google Scholar
Iwaniec, H. and Kowalski, E.. Analytic number theory. Amer. Math. Soc. Colloquium Publications. vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Katz, N. M.. Sommes exponentielles. Astérisque. Société Mathématique de France, Paris, 1980.Google Scholar
Katz, N. M.. Gauss sums, Kloosterman sums, and monodromy group. Ann. Math. Stud. (Princeton University Press, Princeton, NJ, 1988).Google Scholar
Katz, N. M.. Exponential sums and differential equations. Ann. Math. Stud. (Princeton University Press, Princeton, NJ, 1990).Google Scholar
Kowalski, E., Lau, Y.-K., Soundararajan, K. and Wu, J.. On modular signs. Math. Proc. Camb. Phil. Soc. 149(3) (2010), 389–411.CrossRefGoogle Scholar
Kowalski, E. and Sawin, W.. Kloosterman paths and the shape of exponential sums. Compos. Math. 152(7) (2016), 1489–1516.CrossRefGoogle Scholar
Lamzouri, Y.. On the distribution of the maximum of cubic exponential sums. J. Inst. Math. Jussieu 19(4) (2020), 1259–1286.CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C.. Exponential sums with multiplicative coefficients. Invent. Math. 43(1) (1977), 69–82.CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C.. Mean values of character sums. Canad. J. Math. 31(3) (1979), 476–487.CrossRefGoogle Scholar
Pólya, G.. Über die Verteilung der quadratischen Reste und Nichtreste. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (1918), 21–29.Google Scholar
Paley, R. E. A. C.. A Theorem on Characters. J. London Math. Soc. 7(1) (1932), 28–32.CrossRefGoogle Scholar
Perret-Gentil, C.. Gaussian distribution of short sums of trace functions over finite fields. Math. Proc. Camb. Philos. Soc. 163(3) (2017), 385–422.CrossRefGoogle Scholar
Vinogradov, I. M.. Sur la distribution des résidus et non-résidus des puissances. Fiz.-Mat. Ob. Permsk. Gos. Univ. 1, (1918), 94–98.Google Scholar
Weil, A.. On some exponential sums. Proc. Nat. Acad. Sci. U.S.A. 34 (1948), 204–207.CrossRefGoogle ScholarPubMed