Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T07:53:40.937Z Has data issue: false hasContentIssue false
  • English
  • Français

On the size of linearization domains

Published online by Cambridge University Press:  01 September 2008

XAVIER BUFF  and
CARSTEN L. PETERSEN
XAVIER BUFF
Affiliation:
Institut de Mathématiques, Université Paul Sabatier, 118, route de Narbonne, 31062 Toulouse Cedex 9, France.
CARSTEN L. PETERSEN
Affiliation:
IMFUFA at NSM, Roskilde University, Universitetsvej 1, Postbox 260, DK-4000 Roskilde, Denmark.
Get access Rights & Permissions [Opens in a new window]

Abstract

Assume 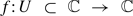is a holomorphic map fixing 0 with derivative λ, where 0 < |λ| ≤ 1. If λ is not a root of unity, there is a formal power series φf(z) = z + 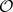(z2) such that φf(λ z) = f(φf(z)). This power series is unique and we denote by Rconv(f) ∈ [0,+∞] its radius of convergence. We denote by Rgeom(f) the largest radius r ∈ [0, Rconv(f)] such that φf(D(0,r)) ⊂ U. In this paper, we present new elementary techniques for studying the maps f ↦ Rconv(f) and f ↦ Rgeom(f). Contrary to previous approaches, our techniques do not involve studying the arithmetical properties of rotation numbers.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 145 , Issue 2 , September 2008 , pp. 443 - 456
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[ABC]Avila, A., Buff, X. and Chéritat, A.. Siegel disks with smooth boundaries. Acta Math. 193 (2004), 1–30.CrossRefGoogle Scholar
[BC1]Buff, X. and Chéritat, A.. The Brjuno function continuously estimates the size of siegel disks. Annals of Math. 164 (2006), 265–312.CrossRefGoogle Scholar
[BC2]Buff, X. and Chéritat, A.. A new proof of a conjecture of Yoccoz. Preprint (2007).Google Scholar
[C]Chéritat, A.. Recherche dénsembles de Julia de mesure de Lebesgue positive. PhD. Thesis (2001).Google Scholar
[DH]Douady, A. and Hubbard, J. H.. On the dynamics of polynomial-like mappings. Ann. Sci. ENS Paris 18 (1985), 287–343.Google Scholar
[G]Gumenuk, P.. Carathéodory convergence of immediate basins of attraction to a Siegel disk. Preprint (2006).Google Scholar
[Ri]Risler, E.. Linéarisation des perturbations holomorphes des rotations et applications. Mém. Soc. Math. Fr. (N.S.) 77 (1999).Google Scholar
[Y]Yoccoz, J. C.. Petits diviseurs en dimension 1. Astérisque 231 (1995).Google Scholar