Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-29T18:55:07.076Z Has data issue: false hasContentIssue false
  • English
  • Français

On the shifted eigenvalue problem

Published online by Cambridge University Press:  24 October 2008

R. J. Bell  and
P. Dean
R. J. Bell
Affiliation:
Division of Numerical and Applied Mathematics, National Physical Laboratory, Teddington, Middlesex
P. Dean
Affiliation:
Division of Numerical and Applied Mathematics, National Physical Laboratory, Teddington, Middlesex
Get access Rights & Permissions [Opens in a new window]

Extract

Lanczos(1, 2) has considered the shifted eigenvalue problem where C is a (p × q) matrix of rank r, CH is its hermitean conjugate and u, v are column vectors of orders p, q respectively. In this note we extend Lanczos' work to cover the more general eigenvalue problem 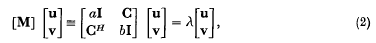which arises in certain problems in solid state physics (3). In (2), the I's are unit matrices of appropriate orders and the constants a, b are real; the partitioned matrix M is thus hermitean so that its eigenvalues λ are real.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 1 , January 1970 , pp. 97 - 99
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Lanozos, C.Amer. Math. Monthly, 65 (1958), 665.Google Scholar
(2)Lanozos, C.Proc. Inter. Congress of Mathematicians, p. 154. Cambridge Univ. Press, 1958.Google Scholar
(3)Bell, R. J. and Dean, P. J.Inst. Math. Appl. (to appear).Google Scholar