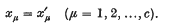Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kokilashvili, V. M.
1987.
Weighted Inequalities for Maximal Functions and Fractional Integrals in Lorentz Spaces.
Mathematische Nachrichten,
Vol. 133,
Issue. 1,
p.
33.
Lamont, P. J. C.
1991.
Unique factorization in Cayley arithmetics and cryptology.
Glasgow Mathematical Journal,
Vol. 33,
Issue. 3,
p.
267.
Ono, Ken
Robins, Sinai
and
Wahl, Patrick T.
1995.
On the representation of integers as sums of triangular numbers.
Aequationes Mathematicae,
Vol. 50,
Issue. 1-2,
p.
73.
Ono, Ken
Robins, Sinai
and
Wahl, Patrick T.
1995.
Aggregating clones, colors, equations, iterates, numbers, and tiles.
p.
73.
Milne, Stephen C.
1996.
New infinite families of exact sums of squares formulas, Jacobi elliptic functions, and Ramanujan’s tau function.
Proceedings of the National Academy of Sciences,
Vol. 93,
Issue. 26,
p.
15004.
Milne, Stephen C.
2002.
Infinite Families of Exact Sums of Squares Formulas, Jacobi Elliptic Functions, Continued Fractions, and Schur Functions.
Vol. 5,
Issue. ,
p.
7.
Ballantine, Cristina
and
Merca, Mircea
2019.
Jacobi’s Four and Eight Squares Theorems and Partitions into Distinct Parts.
Mediterranean Journal of Mathematics,
Vol. 16,
Issue. 2,



 are only considered to be the same solution if
are only considered to be the same solution if