Hostname: page-component-7479d7b7d-wxhwt Total loading time: 0 Render date: 2024-07-09T12:13:44.228Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Real Zeros of a certain Trigonometric Function

Published online by Cambridge University Press:  24 October 2008

P. Stein
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose that a, c and A are real, and that

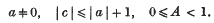
Let n (X) be the number of zeros of

in 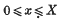; then it is not difficult to prove that

for some K = K (A, a, c, θ). The problem in this paper is to determine the function K explicitly in terms of its variables.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 31 , Issue 4 , October 1935 , pp. 455 - 467
Copyright
Copyright © Cambridge Philosophical Society 1935

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† γ is restricted by 0≤γ<1, while η is not so restricted. Corresponding, however, to any η satisfying the conditions of the Lemma there is a γ for which either γ = η or γ = η ± 1.

‡ For if γ and z are real, then

‡ The result may be obtained more easily by an appeal to the maximum modulus principle for a complex function

and is bounded, since η, β 1 and a 1 are bounded.

† See (1.1.4).

† In the case A = A′, f(x) has a double zero at x = x 1.

‡ In the case b 2 ≠ 0, f′(x 1) = 0, f″(x 1) = 0, it may be shown that f‴(x 1)╪0. Hence f(x) has a triple zero at x = x 1.

§ Neglecting the trivial case θ = 1.

† For this gives 0≤ξ<q.

‡ By Lemma 5.