Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T04:20:06.621Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Quantum Theory of Vibration-Rotation Bands

Published online by Cambridge University Press:  24 October 2008

J. R. Oppenheimer
Get access Rights & Permissions [Opens in a new window]

Extract

The dynamical problem of the “diatomic molecule” is solved on the new mechanics. The terms of the rotational energy are 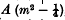, where 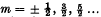; the weights of the corresponding states are 2m; the frequencies differ a little from the classical ones. Finally the intensities are slightly different from those computed by Kemble; the main term agrees with that of Fowler, but the positive branch is only slightly stronger than the negative. The central line vanishes. The intensities are valid only for the fundamental band.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 23 , Issue 3 , July 1926 , pp. 327 - 335
Copyright
Copyright © Cambridge Philosophical Society 1926

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Fowler, , Phil. Mag. vol. XLIX, p. 1272 (1925).CrossRefGoogle Scholar

† Kemble, , Phys. Rev. vol. xxv, p. 1 (1925).CrossRefGoogle Scholar

‡ Dirac, , Proc. Roy. Soc. A, vol. cx, p. 561 (1926)CrossRefGoogle Scholar; Born, , Heisenberg, , Jordan, , Zeit. f. Physik, vol. xxxv, p. 557 (1926).CrossRefGoogle Scholar

§ Brillouin, , C.R. vol. CLXXXII, p. 374 (1926).Google Scholar

| Heisenberg, , Zeit. f. Physik, vol. xxx, p. 879 (1925)CrossRefGoogle Scholar; Born, und Jordan, , Zeit. f. Physik, vol. xxxiv, p. 858 (1925).CrossRefGoogle Scholar

* Dirac, , Proc. Roy. Soc. A, vol. cx, p. 561 (1926).CrossRefGoogle Scholar

† Kemble, , Phys. Rev. vol. xxv, p. 1 (1925).CrossRefGoogle Scholar

‡ Heisenberg, , Zeit. f. Physik, vol. XXXIII, p. 879 (1925)CrossRefGoogle Scholar; Born, und Jordan, , Zeit. f. Physik, vol. xxxiv, p. 858 (1925).CrossRefGoogle Scholar

* Dirac, , Proc. Roy. Soc. A, vol. cx, p. 561 (1926)CrossRefGoogle Scholar; Born, , Heisenberg, , Jordan, , Zeit. f. Physik, vol. xxxv, p. 557 (1926).CrossRefGoogle Scholar

† Dirac, , Proc. Roy. Soc. A, vol. cxi, p. 281 (1926).CrossRefGoogle Scholar

‡ Born, , Atommechanik, § 20.Google Scholar

* Dirac, , Proc. Roy. Soc. A, vol. cxi, p. 281 (1926).CrossRefGoogle Scholar

† Dirac, , Proc. Roy. Soc. A, vol. cx, p. 561 (1926)CrossRefGoogle Scholar; Born, , Heisenberg, , Jordan, , Zeit. f. Physik, vol. xxxv, p. 557 (1926).CrossRefGoogle Scholar

* On Schrodinger's Theory there is no normal state for a rigid rotator in two dimensions, and the transitions for m, (½→½), (−½→½) occur.

* Kemble, , loc.cit. and Fowler , Phil. Mag. vol. L, p. 1079 (1925).Google Scholar

† For the fundamental hydrogen chloride band studied by Kemble and Fowler the values of 4γ and differ by only about 10 per cent.; the positive branch remains slightly the stronger.

* Schrödinger, , Ann. A. Phys. vol. LXXIX, p. 484 (1926). See particularly Eq. (51).Google Scholar

† Mensing, , Zeit. f. Physik, vol. xxxvi, p. 814 (1926).CrossRefGoogle Scholar

‡ Born, und Jordan, , Zeit. f. Physik, vol. xxxiv, p. 838 (1925).Google Scholar