Published online by Cambridge University Press: 24 October 2008
Let ξ, η, ζ be linear forms in u, v, w with real coefficients and determinant Δ ≠ 0. A conjecture of Minkowski, which was subsequently proved by Remak, tells us that for any real numbers a, b, c there exist integral values of u, v, w for which
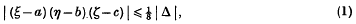
and the constant ⅛ on the right is best possible.
* J. London Math. Soc. 14 (1939), 47–51.Google Scholar
† When making this suggestion, Prof. Mordell told me that he had proved (3) for the linear forms (4) with a value of ![]() appreciably less than ⅛.
appreciably less than ⅛.
* See Davenport, , Proc. Cambridge Phil. Soc. 39 (1942), 1–21CrossRefGoogle Scholar and references given there.
† Proc. K. Akad. Wet. Amsterdam, 49 (1946), 815–821.Google Scholar
* The field k(θ) is, of course, galoisian, and is transformed into itself by θ → ø, which implies ø → ψ and ψ → θ.
† We name θ ø, ψ so that
* See the previous footnote.
* This field has the same properties as those stated for k(θ) in an earlier footnote.
† We name θ′ ø′, ψ′ so that