Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-16T17:24:50.791Z Has data issue: false hasContentIssue false
  • English
  • Français

On the product of three non-homogeneous linear forms

Published online by Cambridge University Press:  24 October 2008

L. E. Clarke
L. E. Clarke
Affiliation:
University CollegeLondon
Get access Rights & Permissions [Opens in a new window]

Extract

Let ξ, η, ζ be linear forms in u, v, w with real coefficients and determinant Δ ≠ 0. Then there exists a number ℳ such that, corresponding to any real numbers a, b, c, there exist rational integers u, v, w for which

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 47 , Issue 2 , April 1951 , pp. 260 - 265
Copyright
Copyright © Cambridge Philosophical Society 1951

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

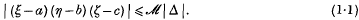
* Remak, R.Math. Z. 17 (1923), 1–34CrossRefGoogle Scholar, and 18 (1923), 173–200.

† Davenport, H.J. London Math. Soc. 14 (1939), 47–51.CrossRefGoogle Scholar

‡ Davenport, H.Proc. Cambridge Phil. Soc. 43 (1947), 137–52.CrossRefGoogle Scholar

§ Prasad, A. V.Proc. K. Akad. Wet. Amsterdam, 52 (1949), 55–65 and 112–24.Google Scholar

∥ See Table II of Reid's, L. W. thesis Tafel der Klassenanzahlen für kubische Zahlkörper (Göttingen, 1899).Google Scholar

* Davenport, H.Proc. Cambridge Phil. Soc. 43 (1947), 137–52.CrossRefGoogle Scholar