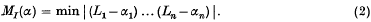Let L1, …, Ln be n homogeneous linear forms in n variables u1, …, un, with non-zero determinant Δ. Suppose that L1, …, Lr have real coefficients, that Lr+1, …, Lr+s have complex coefficients, and that the form Lr+s+j is the complex conjugate of the form Lr+j for j = 1, …, s, where r + 2s = n. Let

for integral u1, …, un, not all zero. For any n numbers α1, …, αn of the same ‘type’ as the forms L1, …, Ln (that is, α1, …, αr real, αr+1, …, αr+s complex, αr+s+j = ᾱr+j), let