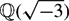Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-30T22:17:32.128Z Has data issue: false hasContentIssue false
  • English
  • Français

On the p-part of the Birch–Swinnerton-Dyer conjecture for elliptic curves with complex multiplication by the ring of integers of $\mathbbQ(\sqrt-3)$

Published online by Cambridge University Press:  17 October 2016

YUKAKO KEZUKA
YUKAKO KEZUKA*
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Cambridge, CB3 0WA. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study infinite families of quadratic and cubic twists of the elliptic curve E = X0(27). For the family of quadratic twists, we establish a lower bound for the 2-adic valuation of the algebraic part of the value of the complex L-series at s=1, and, for the family of cubic twists, we establish a lower bound for the 3-adic valuation of the algebraic part of the same L-value. We show that our lower bounds are precisely those predicted by the celebrated conjecture of Birch and Swinnerton-Dyer.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 164 , Issue 1 , January 2018 , pp. 67 - 98
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Cassels, J.W.S. and Fröhlich, A. Algebraic Number Theory. London Math. Soc., 2nd Edition (2010).Google Scholar
[2] Coates, J. and Wiles, A. On the conjecture of Birch and Swinnerton-Dyer. Invent. Math. 39 (1977), pp. 223–251.Google Scholar
[3] Goldstein, C. and Schappacher, N. Séries d'Eisenstein et fonctions L de courbes elliptiques à multiplication complexe. J. Reine Angew. Math. 327 (1981), pp. 184–218.Google Scholar
[4] Rubin, K. The “main conjectures” of Iwasawa theory for imaginary quadratic fields. Invent. Math. 103 (1991) pp. 25–68.CrossRefGoogle Scholar
[5] Silverman, J. H. The Arithmetic of Elliptic Curves, 2nd Edition. Graduate Texts in Math. vol. 106 (Springer–Verlag, 2006).Google Scholar
[6] Stephens, N. M. The diophantine equation X 3+Y 3=DZ 3 and the conjectures of Birch and Swinnerton-Dyer, J. Reine Angew. Math. 231 (1968), pp. 121–162.Google Scholar
[7] Tate, J. Algorithm for determining the type of a singular fiber in an elliptic pencil. Modular Functions of One Variable IV. Lecture Notes in Math. vol. 476 (Springer, 1975), pp. 33–52.Google Scholar
[8] Zhao, C. A criterion for elliptic curves with second lowest 2-power in L(1). Math. Proc. Camb. Phil. Soc. 131 (2001), pp. 385–404.CrossRefGoogle Scholar
[9] Zhao, C. A criterion for elliptic curves with lowest 2-power in L(1) (II). Math. Proc. Camb. Phil. Soc. 134 (2003), pp. 407–420.Google Scholar