Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T14:11:56.307Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Number of Real Roots of a Random Algebraic Equation

Published online by Cambridge University Press:  24 October 2008

G. Samal
G. Samal
Affiliation:
Department of MathematicsBirkbeck CollegeLondon
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Nn be the number of real roots of a random algebraic equation 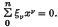The coefficients ξν are independent random variables identically distributed with expectation zero; the variance and third absolute moment are finite and non-zero. It is proved that

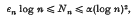
where εν tends to zero, but εν log n tends to infinity. The measure of the exceptional set tends to zero as n tends to infinity.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 3 , July 1962 , pp. 433 - 442
Copyright
Copyright © Cambridge Philosophical Society 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Berry, A. C., The accuracy of the Gaussian approximation to the sum of independent variates. Trans. American Math. Soc. 49 (1941), 122–136.CrossRefGoogle Scholar
(2)Cramer, H., Random variables and probability distributions (Cambridge Tract in Mathematics, no. 36; Cambridge University Press, 1937).Google Scholar
(3)Erdős, P., and Offord, A. C., On the number of real roots of a random algebraic equation. Proc. London Math. Soc. (3), 6 (1956), 139–160.Google Scholar
(4)Esseen, C. G., Fourier analysis of distribution functions. Acta Math. 77 (1945), 1–125.CrossRefGoogle Scholar
(5)Kac, M., On the average number of real roots of a random algebraic equation. Bull. American Math. Soc. 49 (1943), 314–320.Google Scholar
(6)Kac, M., On the average number of real roots of a random algebraic equation. II. Proc. London Math. Soc. (2) 50 (1949), 390–408.Google Scholar
(7)Littlewood, J. E. and Offord, A. C., On the number of real roots of a random algebraic equation. II. Proc. Cambridge Philos. Soc. 35 (1939), 133–148.CrossRefGoogle Scholar
(8)Offord, A. C., An inequality for sums of independent random variables. Proc. London Math. Soc. (2) 48 (1945), 467–477.Google Scholar