Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T14:49:01.237Z Has data issue: false hasContentIssue false
  • English
  • Français

On the least non-residue of a quartic polynomial

Published online by Cambridge University Press:  24 October 2008

Kenneth S. Williams
Kenneth S. Williams
Affiliation:
University of Manchester
Get access Rights & Permissions [Opens in a new window]

Extract

Let p be a prime and let f(x) be a quartic polynomial with integral coefficients. I consider the problem of estimating the least non-negative non-residue k of f(x) (modp) (I omit the mod p hereafter), for large primes p, so f(x) ≡ r has a solution for

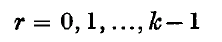
but not for r = k. The same problem for cubics has been considered by Mordell ((1)), who showed that

as p → ∞, where the constant implied in the O-symbol is independent of the coefficients of the cubic. In fact a more detailed examination of Mordell's proof gives the better estimate

It is the purpose of this paper to show that this same estimate also holds for quartic polynomials.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 3 , July 1966 , pp. 429 - 431
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Mordell, L. J.On the least residue and non-residue of a polynomial. J. Lond. Math. Soc. 38 (1963), 451–453.CrossRefGoogle Scholar
(2)Пe;pejibmytep, Г. И.O hekotopБix cymmax c xapaktepamи. Ycnexu mamei.amuчeckux Hayk, 18 (1963), 145–149.Google Scholar
(3)Stickelberger, L.Verhand. I. Internal. Math. Kongress (1897), 186 (see L. E. Dickson, History of the theory of numbers, vol. 1, 249).Google Scholar