Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T23:38:38.006Z Has data issue: false hasContentIssue false
  • English
  • Français

On the invariance of the essential spectrum of an arbitrary operator. III

Published online by Cambridge University Press:  24 October 2008

Martin Schechter
Martin Schechter
Affiliation:
Belfer Graduate School of Science, Yeshiva University
Get access Rights & Permissions [Opens in a new window]

Extract

The spectrum of the hydrogen energy operator

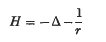
(Δ is the Laplacian and r is the distance from the origin) consists of the non-negative real axis and a sequence of negative eigenvalues of finite multiplicities converging to O. In the present study we are interested in finding sufficient conditions on a potential q(x) such that the spectrum of the operator

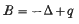
in En has a ‘hydrogen-like’ spectrum, i.e. a spectrum consisting of

(a) the non-negative real axis,

(b) at most a denumerable set of negative eigenvalues of finite multiplicities having zero as its only possible limit point.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 4 , October 1968 , pp. 975 - 984
Copyright
Copyright © Cambridge Philosophical Society 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Kato, Tosio. Fractional powers of dissipative operators. J. Math. Soc. Japan 13 (1961), 246–274.CrossRefGoogle Scholar
(2)Schechter, M.On the invariance of the essential spectrum of an arbitrary operator. II. Richerche Mat. 16 (1967), 3–26.Google Scholar
(3)Wolf, F.On the essential spectrum of partial differential boundary problems. Comm. Pure Appl. Math. 12 (1959), 211–228.CrossRefGoogle Scholar
(4)Wolf, F.On the invariance of the essential spectrum under a change of boundary conditions of partial differential boundary operators. Indag. Math. 21 (1959), 142–315.CrossRefGoogle Scholar
(5)Schechter, M.On the essential spectrum of an arbitrary operator. J. Math. Anal. Appl. 13 (1966), 205–215.CrossRefGoogle Scholar
(6)Browder, F. E.On the spectral theory of elliptic differential operators. I. Math. Ann. 142 (1961), 22–130.CrossRefGoogle Scholar
(7)Hörmander, Lars. Linear partial differential operators (Springer-Verlag, Berlin, 1963).CrossRefGoogle Scholar
(8)Rejto, P. A.On the essential spectrum of the hydrogen energy and related operators. Pacific J. Math. 19 (1966), 109–140.CrossRefGoogle Scholar
(9)Balslev, E.The essential spectrum of self-adjoint elliptic differential operators in L 2(Rn). Math. Scand. 19 (1966), 193–210.CrossRefGoogle Scholar
(10)Birman, M. S.On the spectrum of singular boundary value problems. Mat. Sb. 97 (1961), 125–174.Google Scholar