Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T14:29:57.362Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Grothendieck ring of varieties

Published online by Cambridge University Press:  18 January 2015

AMIT KUBER
AMIT KUBER*
Affiliation:
School of Mathematics, University of Manchester, Manchester M13 9PL e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K0(Vark) denote the Grothendieck ring of k-varieties over an algebraically closed field k. Larsen and Lunts asked if two k-varieties having the same class in K0(Vark) are piecewise isomorphic. Gromov asked if a birational self-map of a k-variety can be extended to a piecewise automorphism. We show that these two questions are equivalent over any algebraically closed field. If these two questions admit a positive answer, then we prove that its underlying abelian group is a free abelian group and that the associated graded ring of the Grothendieck ring is the monoid ring 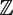$\mathbb{Z}$[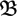$\mathfrak{B}$] where 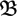$\mathfrak{B}$ denotes the multiplicative monoid of birational equivalence classes of irreducible k-varieties.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 158 , Issue 3 , May 2015 , pp. 477 - 486
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abramovich, D., Karu, K., Matsuki, K. and Włodarczyk, J.. Torification and factorisation of birational maps. J. Amer. Math. Soc. 15 (3) (2002), 531–572.CrossRefGoogle Scholar
[2]Beke, T.. The Grothendieck ring of varieties and of the theory of algebraically closed fields, preprint.Google Scholar
[3]Bittner, F.. The universal Euler characteristic for varieties of characteristic zero. Compositio Math. 15 (4) (2004), 1011–1032.Google Scholar
[4]Gromov, M.. Endomorphisms of symbolic algebraic varieties. J. Eur. Math. Soc. 15 (2) (1999), 109–197.Google Scholar
[5]Kollár, J.. Conics in the Grothendieck ring. Adv. Math. 15 (1) (2005), 27–35.CrossRefGoogle Scholar
[6]Krajicěk, J. and Scanlon, T.. Combinatorics with definable sets: Euler characteristics and Grothendieck rings. Bull. Symb. Logic 15 (3) (2000), 311–330.Google Scholar
[7]Lamy, S. and Sebag, J.. Birational self-maps and piecewise algebraic geometry. J. Math. Sci. -Univ. Tokyo 15 (3) (2012), 325–357.Google Scholar
[8]Larsen, M. and Lunts, V. A.. Motivic measures and stable birational geometry. Mosc. Math. J. 15 (1) (2003), 85–95.CrossRefGoogle Scholar
[9]Liu, Q. and Sebag, J.. The Grothendieck ring of varieties and piecewise isomorphisms. Math. Z. 15 (2) (2010), 321–342.Google Scholar
[10]Poonen, B.. The Grothendieck ring of varieties is not a domain. Math. Res. Lett. 15 (4) (2002), 493–497.Google Scholar
[11]Sahasrabudhe, N.. Grothendieck ring of varieties. Master's thesis Université de Bordeaux (2007) available at http://www.algant.eu/documents/theses/neeraja.pdf.74.Google Scholar
[12]Sebag, J.. Variations on a question of Larsen and Lunts. Proc. Amer. Math. Soc. 15 (4) (2010), 1231–1242.Google Scholar
[13]Weibel, C.. The K-book: an introduction to algebraic K-theory. Grad. Studies in Math. 15 (American Mathematical Society, 2013).Google Scholar