Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-27T11:56:39.469Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Fourier series of a finitely described convex curve and a conjecture of H. S. Shapiro

Published online by Cambridge University Press:  24 October 2008

T. Sheil-Small
T. Sheil-Small
Affiliation:
Department of Mathematics, University of York, York YO1 5DD
Get access Rights & Permissions [Opens in a new window]

Abstract

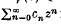Let F(eis) denote a homeomorphism of the positively oriented unit circle onto a convex curve Γ and let f (eit) = F(eiΦ(t)), where Φ(t) is a non-decreasing function such that Φ(2π) – Φ(0) ≤ 2πN (N a positive integer). If f (eit) has Fourier coefficients cn, we show that is either constant or an N -valent analytic function in {|z| < 1}. We prove that 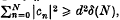where d is the distance from 0 to Γ and δ(N) > 0 depends only on N. This settles affirmatively a conjecture of H. S. Shapiro.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 98 , Issue 3 , November 1985 , pp. 513 - 527
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Anderson, J. M., Barth, K. F. and Brannan, D. A.. Research problems in complex analysis. Bull. London Math. Soc. 9 (1977), 129–162.CrossRefGoogle Scholar
[2]Choquet, G.. Sur un type de transformation analytique généralisant la représentation conforme et définie au moyen de fonctions harmoniques. Bull. Sci. Math. 2 (69) (1945), 156–165.Google Scholar
[3]Clunie, J. and Sheil-Small, T.. Harmonic univalent functions. Ann. Acad. Sci. Fenn. Series A.I. Math. 9 (1984), 3–25.CrossRefGoogle Scholar
[4]Hall, R. R.. On a conjecture of Shapiro about trigonometric series. J. London Math. Soc. (2) 25 (1982), 407–415.CrossRefGoogle Scholar
[5]Hall, R. R.. On an inequality of E. Heinz. J. Analyse Math. 42 (1983), 185–198.CrossRefGoogle Scholar
[6]Heinz, E., Über die Lösungen der Minimalflächengleichung. Nachr. Akad. Wiss. Göringen Math. Phys. Kl. (1952), 51–56.Google Scholar
[7]Hummel, J. A.. Multivalent starlike functions. J. Analyse Math. 18 (1967), 133–160.CrossRefGoogle Scholar
[8]Lyzzaik, A.. Multivalent linearly accessible functions and close-to-convex functions. Proc. London Math. Soc. (3) 44 (1982), 178–192.CrossRefGoogle Scholar
[9]Sheil-Small, T.. Coefficients and integral means of some classes of analytic functions. Proc. Amer. Math. Soc. 88 (1983), 275–282.CrossRefGoogle Scholar
[10]Styer, D.. Close-to-convex multivalent functions with respect to weakly starlike functions. Trans. Amer. Math. Soc. 169 (1972), 105–112.CrossRefGoogle Scholar