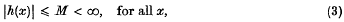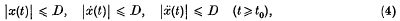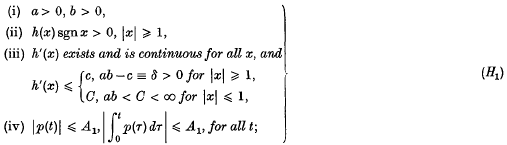Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ezeilo, J. O. C.
1964.
On the existence of almost periodic solutions of some dissipative second order differential equations.
Annali di Matematica Pura ed Applicata,
Vol. 65,
Issue. 1,
p.
389.
Villari, Gaetano
1965.
Contributi allo studio dell'esistenza di soluzioni periodiche per i sistemi di equazioni differenziali ordinarie.
Annali di Matematica Pura ed Applicata,
Vol. 69,
Issue. 1,
p.
171.
Villari, Gaetano
1966.
Soluzioni periodiche di una classe di equazioni differenziali del terz’ ordine quasi lineari.
Annali di Matematica Pura ed Applicata,
Vol. 73,
Issue. 1,
p.
103.
Ezeilo, J. O. C.
and
Tejumola, H. O.
1966.
Boundedness and periodicity of solutions of a certain system of third-order non-linear differential equations.
Annali di Matematica Pura ed Applicata,
Vol. 74,
Issue. 1,
p.
283.
Tejumola, H. O.
1969.
On the boundedness and periodicity of solutions of certain third-order non-linear differential equations.
Annali di Matematica Pura ed Applicata,
Vol. 83,
Issue. 1,
p.
195.
Reissig, Rolf
1970.
On the existence of periodic solutions of a certain non-autonomous differential equation.
Annali di Matematica Pura ed Applicata,
Vol. 85,
Issue. 1,
p.
235.
Mawhin, Jean
1975.
International Conference on Differential Equations.
p.
537.
Chukwu, Ethelbert Nwakuche
1975.
On the boundedness of solutions of third order differential equations.
Annali di Matematica Pura ed Applicata,
Vol. 104,
Issue. 1,
p.
123.
Ezeilo, J. O. C.
1975.
A further result on the existence of periodic solutions of the equation .
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 77,
Issue. 3,
p.
547.
Bereketoglu, H.
1992.
On the periodic solutions of certain class of seventh-order differential equations.
Periodica Mathematica Hungarica,
Vol. 24,
Issue. 1,
p.
13.
Zhang, Zhengqiu
and
Wang, Zhicheng
2002.
Periodic solutions of third-order functional differential equations with variable coefficients.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 17,
Issue. 2,
p.
145.
Zhang, Zhengqiu
and
Wang, Zhicheng
2004.
Periodic solutions of the third order functional differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 292,
Issue. 1,
p.
115.
Mawhin, J.
2005.
10 Mathematical Essays on Approximation in Analysis and Topology.
p.
199.
Song, Bing
Pan, Lijun
Cao, Jinde
and
Wang, Peiguang
2011.
Periodic Solutions for a Class of n‐th Order Functional Differential Equations.
International Journal of Differential Equations,
Vol. 2011,
Issue. 1,
Bereketoglu, Huseyin
Lafci, Mehtap
and
Oztepe, Gizem S.
2017.
On the Oscillation of a Third Order Nonlinear Differential Equation with Piecewise Constant Arguments.
Mediterranean Journal of Mathematics,
Vol. 14,
Issue. 3,
Kong, Fanchao
and
Lu, Shiping
2020.
Positive Periodic Solutions of Singular Third-Order Functional Differential Equations with p-Laplacian-Like Operators.
Mathematical Notes,
Vol. 107,
Issue. 5-6,
p.
759.
Eze, Everestus Obinwanne
Obasi, Uchenna Emmanuel
Ezugorie, Godwin
and
Hannah, Enyiduru Ekwomchi
2023.
Existence, uniqueness, boundedness and stability of periodic solutions of a certain second-order nonlinear differential equation with damping and resonance effects.
Biometrical Letters,
Vol. 60,
Issue. 2,
p.
109.