Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-20T08:36:20.405Z Has data issue: false hasContentIssue false
  • English
  • Français

On the equations defining tangent cones

Published online by Cambridge University Press:  24 October 2008

Lorenzo Robbiano  and
Giuseppe Valla
Lorenzo Robbiano
Affiliation:
Università di Genova, Italia
Giuseppe Valla
Affiliation:
Università di Genova, Italia
Get access Rights & Permissions [Opens in a new window]

Extract

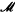This paper treats the local study of singularities by means of their tangent cones, more specifically the study of graded rings associated to an ideal of a local ring. We recall some basic facts: let (R, ) be a local ring, I, J ideals of R, such that J ⊆ I; then GR/J(I / J), the graded ring associated to I / J, is canonically isomorphic to the quotient of GR(I) modulo a homogeneous ideal, which is called J*, and which is generated by the so-called ‘initial forms’ of the elements of J. Let us consider the following example: Let k be a field, R = k[X, Y, Z](x, y, Z), I = (X, Y, Z)R, J the prime ideal generated by fl, f2 where f1 = Y3 − Z2, f2 = YZ − X4. Then

and it is easily seen that J* properly contains the ideal generated by the initial forms f*1f*2 of f1, f2; namely f*1 = − Z2, f*2 = YZ and (Yf1 + Zf2)* = Y4 ∉ (−Z2, YZ).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 88 , Issue 2 , September 1980 , pp. 281 - 297
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bennett, B. M.Normally flat deformations. Trans. Amer. Math. Soc. 225 (1977), 1–57.CrossRefGoogle Scholar
(2)Berge, C.Théorie des graphes et ses applications (Paris, Dunod, 1967).Google Scholar
(3)Eagon, J. and Northcott, D. G.Ideals defined by matrices and a certain complex as-sociated with them. Proc. Royal Soc., Sect. A, 269 (1962), 188–204.Google Scholar
(4)Herzog, J.Generators and relations of abelian semigroups and semigroups rings. Manuscripta Math. 3 (1970), 175–193.CrossRefGoogle Scholar
(5)Hironaka, H.Resolution of singularities of an algebraic variety over a field of characteristic 0. Ann. of Math. 79 (1964), 109–326.CrossRefGoogle Scholar
(6)Mora, F. Un algoritmo per la determinazione del cono tangente di una classe di curve. (In preparation.)Google Scholar
(7)Northcott, D. G.Some remarks on the theory of ideals defined by matrices. Quart. J. Math. Oxford (2), 14 (1963), 193–204.CrossRefGoogle Scholar
(8)Renschuch, B.Elementare und praktische Idealtheorie. Mathematik für Lehrer, Band 16 (Berlin, DVW, 1976).Google Scholar
(9)Ryser, H. J.Combinatorial mathematics. The Carus Mathematical Monographs, no. 14 (Wiley, 1963).CrossRefGoogle Scholar
(10)Sally, J. Super regular sequences. (Preprint.)Google Scholar
(11)Valabrega, P. and Valla, G.Form rings and regular sequences. Nagoya Math. J. 72 (1978).CrossRefGoogle Scholar