Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T13:44:24.184Z Has data issue: false hasContentIssue false
  • English
  • Français

On the converse of Mertens' theorem

Published online by Cambridge University Press:  24 October 2008

K. A. Jukes
K. A. Jukes
Affiliation:
Queen's University, Belfast
Get access Rights & Permissions [Opens in a new window]

Extract

Let (λm), (µn) (m, n = 0, 1, 2,…) satisfy

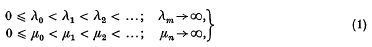
respectively. Let vp (p = 0, 1, 2, …) be the sequence (λm+µn) arranged in ascending order, equal sums λm+µn being considered as giving just one vp Then for given formal series Σam, Σbn the formal series C = Σ cp where

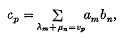
is called the general Dirichlet product of Σamand Σbn (see Hardy (2), p. 239). When λn = µn = n we have the Cauchy product. In the case λn = logm, µn = logn (m, n = 1, 2,…) we have vp =log p(p = 1, 2, …)and it is natural to call C the ordinary Dirichlet product.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 73 , Issue 3 , May 1973 , pp. 467 - 471
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cooke, R. G.Infinite matrices and sequence spaces (Macmillan, 1950).Google Scholar
(2)Hardly, G. H.Divergent series (Oxford, 1949).Google Scholar
(3)Jukes, K. A.On the Ingham and (D, h(n)) summation methods. J. London Math. Soc. 3 (1971), 699–710.CrossRefGoogle Scholar
(4)Schur, I.Über lineare Transformationen in der Theorie der unendilichen Reihen. J. Reins Angew. Math. 151 (1920), 79–111.Google Scholar
(5)Stieltjes, T. J.Note sur la multiplication de deux series. Nouvelles Annales 6 (1887), 210–215.Google Scholar
(6)Wintner, A.Eratosthenian averages (Baltimore, 1943).Google Scholar