Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bolotov, Dmitry
and
Dranishnikov, Alexander
2009.
On Gromov’s scalar curvature conjecture.
Proceedings of the American Mathematical Society,
Vol. 138,
Issue. 4,
p.
1517.
Rudyak, Yuli B.
2010.
On higher analogs of topological complexity.
Topology and its Applications,
Vol. 157,
Issue. 5,
p.
916.
Oprea, John
and
Strom, Jeff
2010.
Lusternik–Schnirelmann category, complements of skeleta and a theorem of Dranishnikov.
Algebraic & Geometric Topology,
Vol. 10,
Issue. 2,
p.
1165.
Dranishnikov, A. N.
2011.
Macroscopic dimension and essential manifolds.
Proceedings of the Steklov Institute of Mathematics,
Vol. 273,
Issue. 1,
p.
35.
Dranishnikov, Alexander
2011.
On macroscopic dimension of rationally essential manifolds.
Geometry & Topology,
Vol. 15,
Issue. 2,
p.
1107.
Dranishnikov, Alexander N.
Katz, Mikhail G.
and
Rudyak, Yuli B.
2011.
Cohomological dimension, self-linking, and systolic geometry.
Israel Journal of Mathematics,
Vol. 184,
Issue. 1,
p.
437.
Cárdenas, M.
Lasheras, F.F.
and
Quintero, A.
2013.
The proper Lusternik–Schnirelmann category of semistable one-ended 3-manifolds.
Topology and its Applications,
Vol. 160,
Issue. 5,
p.
720.
Dranishnikov, Alexander
2014.
On Gromov's positive scalar curvature conjecture for duality groups.
Journal of Topology and Analysis,
Vol. 06,
Issue. 03,
p.
397.
Dranishnikov, Alexander N
2015.
The LS category of the product of lens spaces.
Algebraic & Geometric Topology,
Vol. 15,
Issue. 5,
p.
2985.
Dranishnikov, Alexander
2016.
The topological complexity and the homotopy cofiber of the diagonal map for non-orientable surfaces.
Proceedings of the American Mathematical Society,
Vol. 144,
Issue. 11,
p.
4999.
Dranishnikov, Alexander
2017.
On topological complexity of non-orientable surfaces.
Topology and its Applications,
Vol. 232,
Issue. ,
p.
61.
Rudyak, Yuli B.
2017.
Maps of degree 1 and Lusternik–Schnirelmann category.
Topology and its Applications,
Vol. 221,
Issue. ,
p.
225.
Dranishnikov, Alexander
and
Sadykov, Rustam
2019.
The topological complexity of the free product.
Mathematische Zeitschrift,
Vol. 293,
Issue. 1-2,
p.
407.
Farber, Michael
Grant, Mark
Lupton, Gregory
and
Oprea, John
2019.
Bredon cohomology and robot motion planning.
Algebraic & Geometric Topology,
Vol. 19,
Issue. 4,
p.
2023.
Farber, Michael
and
Mescher, Stephan
2020.
On the topological complexity of aspherical spaces.
Journal of Topology and Analysis,
Vol. 12,
Issue. 02,
p.
293.
Cohen, Daniel C.
and
Vandembroucq, Lucile
2021.
On the topological complexity of manifolds with abelian fundamental group.
Forum Mathematicum,
Vol. 33,
Issue. 6,
p.
1403.
Capovilla, Pietro
Löh, Clara
and
Moraschini, Marco
2022.
Amenable category and complexity.
Algebraic & Geometric Topology,
Vol. 22,
Issue. 3,
p.
1417.
Dranishnikov, Alexander
and
Scott, Jamie
2022.
Surgery approach to Rudyak's conjecture.
Topology and its Applications,
Vol. 311,
Issue. ,
p.
107956.
Scott, Jamie
2022.
On the topological complexity of maps.
Topology and its Applications,
Vol. 314,
Issue. ,
p.
108094.
Błaszczyk, Zbigniew
Carrasquel-Vera, José Gabriel
and
Espinosa Baro, Arturo
2022.
On the sectional category of subgroup inclusions and Adamson cohomology theory.
Journal of Pure and Applied Algebra,
Vol. 226,
Issue. 6,
p.
106959.
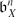 ≠ 0 where
≠ 0 where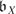 is the Berstein class of X.
is the Berstein class of X.