Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T09:44:12.736Z Has data issue: false hasContentIssue false
  • English
  • Français

On the average order of the lattice rest of a convex planar domain

Published online by Cambridge University Press:  24 October 2008

Werner Georg Nowak
Werner Georg Nowak
Affiliation:
Institut für Mathematik der Universität für Bodenkultur, A-1180 Vienna, Austria
Get access Rights & Permissions [Opens in a new window]

Extract

Let denote a compact convex subset of the Euclidean plane containing the origin as an inner point and assume that the boundary ∂ of is a C∞-image of the 1-torus with finite nonvanishing curvature throughout. As a generalization of the classical circle problem in analytic number theory we consider, for a large parameter t, the number A(t) of lattice points (of the standard lattice ℤ2) in the ‘blown up’ domain 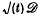and define the ‘lattice rest’ by 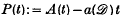(where 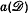is the area of ).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 98 , Issue 1 , July 1985 , pp. 1 - 4
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bochner, S.. Die Poissonsche Summenformel in mehreren Veränderlichen. Math. Ann. 106 (1932), 56–63.CrossRefGoogle Scholar
[2]Bonnesen, T. and Fenchel, W.. Theorie der konvexen Körper (Springer, 1934).Google Scholar
[3]Van Der Corput, J. G.Neue zahlentheoretische Abschätzungen. Math. Ann. 89 (1923), 215–254.CrossRefGoogle Scholar
[4]Fricker, F.. Einführung in die Gitterpunktlehre (Birkhäuser, 1982).CrossRefGoogle Scholar
[5]Hardy, G. H.. On Dirichlet's divisor problem. Proc. London Math. Soc. (2) 15 (1916), 1–25.Google Scholar
[6]Hlawka, E.. Integrale auf konvexen Körpern I. Monatsh. Math. 54 (1950), 1–36.CrossRefGoogle Scholar
[7]Hlawka, E.. Integrale auf konvexen Körpern II. Monatsh. Math. 54 (1950), 81–99.CrossRefGoogle Scholar
[8]Kátai, I.. The number of lattice points in a circle (Russian). Ann. Univ. Sci. Budapest Rolando Eötvös, Sect. Math. 8 (1965), 39–60.Google Scholar
[9]Landau, E.. über die Gitterpunkte in einem Kreise. (Vierte Mitteilung.) Nachr. Königl. Ges. Wiss. Göttingen, math.-phys. Kl. 1923 (1923), 58–65.Google Scholar
[10]Nowak, W. G.. Zur Gitterpunktlehre der euklidischen Ebene. Indag. Math. 46 (1984), 209–223.CrossRefGoogle Scholar
[11]Nowak, W. G.. An Ω-estimate for the lattice rest of a convex planar domain. To appear in Proc. Roy. Soc. Edinburgh, Sect. A.Google Scholar