On the ambiguity in the specification of a two-sheeted surface by its branch curve
Published online by Cambridge University Press: 24 October 2008
Extract
It is familiar that a “double plane”, i.e. an algebraic surface conceived as consisting of each point of a plane counted twice, is unambiguously determined when its “branch curve”, or locus of points in the plane which count as two coincident points of the surface (the general point of the plane counting as two distinct points), is assigned; the only condition which must be satisfied by this curve being that it is of even order. In fact, if f(x, y) = 0 is the Cartesian equation of the curve, the double plane can be regarded as the limit of the surface
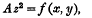
where A is a large constant, or as the projection of this surface, for finite A, from the point at infinity on the z-axis. If, however, f = 0 is of odd order, it is easily seen that the line at infinity also forms part of the branch curve of the double plane. A repeated portion of the branch curve is ineffective, for if φ (x, y) = 0 is any other curve, the surface
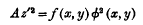
is birationally identical with the former merely by putting
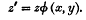
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 30 , Issue 3 , July 1934 , pp. 309 - 314
- Copyright
- Copyright © Cambridge Philosophical Society 1934
References
* Lefschetz, S., L'analysis situs et la géométrie algébrique (1924), p. 82.Google Scholar
† Enriques, F., Ann. di Mat. (4), 1 (1924), 196.Google Scholar
* Veblen, O., Analysis situs (2nd ed., 1931), p. 120.Google Scholar
* Babbage, D. W., Proc. Camb. Phil. Soc. 30 (1934), 297.CrossRefGoogle Scholar
- 2
- Cited by


