Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T14:53:02.033Z Has data issue: false hasContentIssue false
  • English
  • Français

On the absolute summability and convergence of Fourier series and associated series

Published online by Cambridge University Press:  24 October 2008

M. K. Nayak
M. K. Nayak
Affiliation:
Panjab University, Chandigarh—14, India
Get access Rights & Permissions [Opens in a new window]

Extract

1. We suppose that f(t) is integrable L and periodic with period 2π and we denote the Fourier series of f(t) at the point t = x by

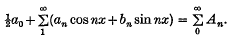
We denote the nth partial sum of the Fourier series by sn. We will prove here a general result (i.e Theorem 1) and some interesting results in connexion with associated series of a Fourier series of the type

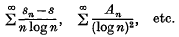
We write

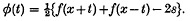
The object of the present paper is to prove the following theorems. (In all the following cases k is any constant > π if nothing else is mentioned.)

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 70 , Issue 3 , November 1971 , pp. 421 - 433
Copyright
Copyright © Cambridge Philosophical Society 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hardy, G. H. and Littlewood, J. E.Some more theorems concerning Fourier Series and Fourier Power Series. Duke Math J. 2 (1936), 354–382 (or Hardy, Collected papers, vol.III, 285–313), Theorem 10.CrossRefGoogle Scholar
(2)Bosanquet, L. S. and Hyslop, J. M.Math. Z. 42 (1937), 489–512, Lemma 10.CrossRefGoogle Scholar
(3)Pollard, S.On the criteria for the convergence of a Fourier series. J. London Math. Soc. 2 (1927), 255–262.CrossRefGoogle Scholar
(4)Kogbetliantz, E.Sur les séries absolument sommables par la méthode des moyennes arithmétiques. Bull. Sci. Math. (2), 49 (1925), 234–256.Google Scholar
(5)Kogbetliantz, E.Sommation des séries et intégrales divergentes par les moyennes arithmétiques et typiques. Mémor. Sci. Math. 52 (1931).Google Scholar
(6)Mohanty, R. and Mohapatra, S.On the absolute convergence of a series associated with a Fourier Series. Proc. Amer. Math. Soc. 7 (1956), 1049–1053.CrossRefGoogle Scholar
(7)Mohanty, R. and Misra, B.On absolute logarithmic summability of a sequence related to a Fourier series, Tôhoku Math. J. (2), 6 (1954), 5–12.CrossRefGoogle Scholar
(8)Mazhar, S. M.A general theorem for absolute Cesaro summability of a series associated with a Fourier Series, Rend. circ. Mat. Palermo (II), 13 (1964).CrossRefGoogle Scholar
(9)Varshney, O. P.On the absolute harmonic summability of a series related to a Fourier series. Proc. Amer. Math. Soc. 10 (1959), 784–789.CrossRefGoogle Scholar