Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hunt, G. A.
1951.
Random Fourier transforms.
Transactions of the American Mathematical Society,
Vol. 71,
Issue. 1,
p.
38.
Walk, Harro
1967.
Symmetrisierte und zentrierte Folgen von Zufallsvariablen.
Mathematische Zeitschrift,
Vol. 102,
Issue. 1,
p.
44.
Marcus, M. B.
and
Pisier, G.
1979.
Séminaire de Probabilités XIII.
Vol. 721,
Issue. ,
p.
72.
Гарсиа-Куерва, Х
Garcia-Cuerva, J
Казарян, Казарос Согомонович
Kazarian, Kazaros Sogomonovich
Коляда, Виктор Иванович
Kolyada, Victor Ivanovich
Торреа, Х Л
and
Torrea, J L
1998.
Неравенство Хаусдорфа - Юнга с векторнозначными коэффициентами и приложения.
Успехи математических наук,
Vol. 53,
Issue. 3,
p.
3.
Talagrand, Michel
2014.
Upper and Lower Bounds for Stochastic Processes.
Vol. 60,
Issue. ,
p.
199.
Sohinger, Vedran
and
Staffilani, Gigliola
2015.
Randomization and the Gross–Pitaevskii Hierarchy.
Archive for Rational Mechanics and Analysis,
Vol. 218,
Issue. 1,
p.
417.
Sohinger, Vedran
2015.
Local existence of solutions to randomized Gross-Pitaevskii hierarchies.
Transactions of the American Mathematical Society,
Vol. 368,
Issue. 3,
p.
1759.
Ronsin, Samuel
Biermé, Hermine
and
Moisan, Lionel
2017.
The Billard Theorem for Multiple Random Fourier Series.
Journal of Fourier Analysis and Applications,
Vol. 23,
Issue. 1,
p.
207.
Guseynov, Yevgeniy
2018.
Summability on non-rectifiable Jordan curves.
Georgian Mathematical Journal,
Vol. 25,
Issue. 2,
p.
249.
Giorgobiani, G.
2019.
Rearrangements of Series.
Journal of Mathematical Sciences,
Vol. 239,
Issue. 4,
p.
437.
S. Alberti, Giovanni
Capdeboscq, Yves
and
Privat, Yannick
2020.
On the randomised stability constant for inverse problems.
Mathematics in Engineering,
Vol. 2,
Issue. 2,
p.
264.
Talagrand, Michel
2021.
Upper and Lower Bounds for Stochastic Processes.
Vol. 60,
Issue. ,
p.
201.
Cheng, Guozheng
Fang, Xiang
and
Liu, Chao
2022.
A Littlewood-Type Theorem for Random Bergman Functions.
International Mathematics Research Notices,
Vol. 2022,
Issue. 14,
p.
11056.
Fan, Aihua
and
Meyer, Yves
2023.
Trigonometric multiplicative chaos and applications to random distributions.
Science China Mathematics,
Vol. 66,
Issue. 1,
p.
3.
Downey, Rodney G.
Greenberg, Noam
and
Tanggara, Andrew
2023.
Algorithmically random series.
Computability,
p.
1.
Esser, Céline
Jaffard, Stéphane
and
Vedel, Béatrice
2024.
Regularity properties of random wavelet series.
Theory of Probability and Mathematical Statistics,
Vol. 110,
Issue. 0,
p.
31.
Fang, Xiang
and
Tien, Pham Trong
2024.
Random analytic functions with a prescribed growth rate in the unit disk.
Canadian Journal of Mathematics,
p.
1.
Cheng, Guozheng
Fang, Xiang
Liu, Chao
and
Lu, Yufeng
2024.
Solid bases and functorial constructions for (p-)Banach spaces of analytic functions.
Proceedings of the Edinburgh Mathematical Society,
Vol. 67,
Issue. 4,
p.
1013.
Cheng, Guozheng
Fang, Xiang
Liu, Chao
and
Lu, Yufeng
2025.
Littlewood-type theorems for random Dirichlet multipliers.
Journal of Functional Analysis,
Vol. 288,
Issue. 12,
p.
110851.



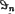 vary independently in the interval (0, 1). What we need is a definition of measure in the space of sequences
vary independently in the interval (0, 1). What we need is a definition of measure in the space of sequences 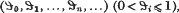 or, what is the same thing, in the space
or, what is the same thing, in the space