No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
1. It is frequently required to find the numerical value of the definite integral 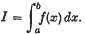 It is, however, often found that even if the analytical expression of f(x) is given, it cannot be integrated in terms of known elementary functions. The elliptic integrals are perhaps the best known examples of functions of this type; and more common are cases where f(x) is not even defined by an analytical expression but merely specified by a table of numerical values. In the two cases mentioned one has to resort to a numerical integration procedure in which the integral is evaluated in terms of the values of f(x) at a finite number of the arguments x1, x2, …, xn. There are essentially two different types of quadrature formulae available, those which depend on the use of finite differences and the tabulation of f(x) at equidistant points, and those which depend on the values of f(x) at suitably selected points xi. These latter, so called mean-value methods, will be discussed in the present paper. For a recent treatment of such methods see, for example, Beard (5).
It is, however, often found that even if the analytical expression of f(x) is given, it cannot be integrated in terms of known elementary functions. The elliptic integrals are perhaps the best known examples of functions of this type; and more common are cases where f(x) is not even defined by an analytical expression but merely specified by a table of numerical values. In the two cases mentioned one has to resort to a numerical integration procedure in which the integral is evaluated in terms of the values of f(x) at a finite number of the arguments x1, x2, …, xn. There are essentially two different types of quadrature formulae available, those which depend on the use of finite differences and the tabulation of f(x) at equidistant points, and those which depend on the values of f(x) at suitably selected points xi. These latter, so called mean-value methods, will be discussed in the present paper. For a recent treatment of such methods see, for example, Beard (5).