No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Any harmonic function which is defined and positive in the half-plane η > 0 may be expressed by
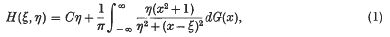
where C is a non-negative number, and G(x) is a bounded non-decreasing function. For a simple proof see Loomis and Widder (2). Let us write

where w(z) is a regular function of z in η > 0, and satisfies the following conditions: (i) w(z) is real and continuous at all points of the open interval (a, b) of the real axis [the interval may be unbounded]; (ii) there exists a simply connected domain Δ, lying in the half-plane η > 0, whose frontier contains the interval (a, b) of the real axis and which is mapped ‘simply’ on the half-plane υ > 0 by the conformal transformation w = w(z).