Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T02:48:27.430Z Has data issue: false hasContentIssue false
  • English
  • Français

On Mellin's inversion formula

Published online by Cambridge University Press:  24 October 2008

J. C. Burkill
J. C. Burkill
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

The extension of Mellin's inversion formula expressed by the equations 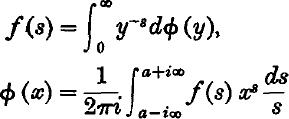has been considered by Fowler who shows that some form of Stieltjes integral is essential to Poincaré's proof of the necessity of the quantum hypothesis. Fowler confines his discussion to a restricted type of function φ (y) which is sufficient for the physical problem. It will be proved here that the formulae hold with a general Stieltjes integral in the first equation.

Type
Articles
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 23 , Issue 4 , October 1926 , pp. 356 - 360
Copyright
Copyright © Cambridge Philosophical Society 1926

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Proc. Royal Soc. (A), vol. 99 (1921), pp. 462–471CrossRefGoogle Scholar. An account of Mellin's formula in the ordinary form (without Stieltjes integrals) is given by Hardy, , Messenger of Math. vol. 47 (1918), pp. 178–184 and vol. 50 (1921), pp. 166–171.Google Scholar

† “The expression in Stieltjes integrals of the inversion formulae of Fourier and Hankel,” Proc. London Math Soc. (unpublished).Google Scholar

* Oppenheim, A., “Some identities in the theory of numbers,” Proc. London Math. Soc. (Records), vol. 24 (1925), p. xxiii. I am indebted to Mr Oppenheim for sending me in MS. the part of his work dealing with discontinuous factors.Google Scholar

† Watson, , Bessel Functions, p. 198.Google Scholar