Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T11:26:08.905Z Has data issue: false hasContentIssue false
  • English
  • Français

On Manin's conjecture for singular del Pezzo surfaces of degree four, II

Published online by Cambridge University Press:  01 November 2007

R. DE LA BRETÈCHE  and
T. D. BROWNING
R. DE LA BRETÈCHE
Affiliation:
Institut de Mathématiques de Jussieu, Université Paris 7 Denis Diderot, Case Postale 7012, 2, Place Jussieu, F-75251 Paris cedex 050 email: [email protected]
T. D. BROWNING
Affiliation:
School of Mathematics, University of Bristol, Bristol BS81TW. email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper establishes the Manin conjecture for a certain non-split singular del Pezzo surface of degree four 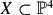. In fact, if U ⊂ X is the open subset formed by deleting the lines from X, and H is the usual projective height function on 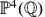, then the height zeta function 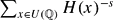is analytically continued to the half-plane ℜe(s) > 17/20.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 143 , Issue 3 , November 2007 , pp. 579 - 605
Copyright
Copyright © Cambridge Philosophical Society 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Batyrev, V. V. and Tschinkel, Y.. Manin's conjecture for toric varieties. J. Algebraic Geom. 7 (1998), 15–53.Google Scholar
[2]Bretèche, R. de la and Browning, T.D.. On Manin's conjecture for singular del Pezzo surfaces of degree four, I. Michigan Math. J. 55 (2007), 51–80.Google Scholar
[3]Browning, T. D.. An overview of Manin's conjecture for del Pezzo surfaces. Gauss–Dirichlet conference (Göttingen 2005), CMI conference proceedings, AMS, to appear.Google Scholar
[4]Chambert-Loir, A. and Tschinkel, Y.. On the distribution of points of bounded height on equivariant compactifications of vector groups. Invent. Math. 148 (2002), 421–452.CrossRefGoogle Scholar
[5]Coray, D. F. and Tsfasman, M. A.. Arithmetic on singular Del Pezzo surfaces. Proc. London Math. Soc. 57 (1988), 25–87.CrossRefGoogle Scholar
[6]Derenthal, U. and Tschinkel, Y.. Universal torsors over del Pezzo surfaces and rational points. Equidistribution in Number Theory: An Introduction (Montreal, 2005), 169–196, NATO Science Series II: Math, Physics and Chemistry 237, Springer, 2006.Google Scholar
[7]Franke, J., Manin, Y. I. and Tschinkel, Y.. Rational points of bounded height on Fano varieties. Invent. Math. 95 (1989), 421–435.CrossRefGoogle Scholar
[8]Heath-Brown, D. R.. Mean values of the zeta-function and divisor problems. Recent progress in analytic number theory, Vol. I, 115–119, Academic Press, 1981.Google Scholar
[9]Heath-Brown, D. R.. Weyl's inequality, Hua's inequality and Waring's problem. J. London Math. Soc. 38 (1988), 2, 216–230.Google Scholar
[10]Hassett, B. and Tschinkel, Y.. Universal torsors and Cox rings. Arithmetic of higher-dimensional algebraic varieties (Palo Alto, 2002), 149–173, Progr. Math. 226, Birkhäuser, 2004.CrossRefGoogle Scholar
[11]Hodge, W. V. D. and Pedoe, D.. Methods of algebraic geometry. Vol. 2, Cambridge University Press, 1952.Google Scholar
[12]Lipman, J.. Rational singularities, with applications to algebraic surfaces and unique factorization. Inst. Hautes études Sci. Publ. Math. 36 (1969), 195–279.Google Scholar
[13]Montgomery, H. L. Topics in multiplicative number theory. Springer Lecture Notes 227, Springer, 1971.Google Scholar
[14]Peyre, E.. Hauteurs et mesures de Tamagawa sur les variétés de Fano. Duke Math. J. 79 (1995), 101–218.CrossRefGoogle Scholar
[15]Swinnerton-Dyer, P.. Counting points on cubic surfaces, II. Geometric methods in algebra and number theory, 303–310, Progr. Math. 235, Birkhäuser, 2005.Google Scholar
[16]Titchmarsh, E. C.. The theory of the Riemann zeta-function. 2nd ed., edited by Heath-Brown, D.R., Oxford University Press, 1986.Google Scholar
[17]Vaaler, J. D.. Some extremal functions in Fourier analysis. Bull. Amer. Math. Soc. 12 (1985), 2, 183–216.Google Scholar