Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T14:29:47.905Z Has data issue: false hasContentIssue false
  • English
  • Français

On loci which have two systems of generating spaces

Published online by Cambridge University Press:  24 October 2008

H. W. Richmond  and
F. Bath
H. W. Richmond
Affiliation:
King's College
F. Bath
Affiliation:
King's College
Get access Rights & Permissions [Opens in a new window]

Extract

In hypergeometry loci defined by parametric equations

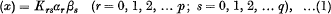
have been frequently discussed from various points of view. Among other properties these loci possess two systems of generating spaces obtained by keeping the α's (or β's) fixed while the β's (or α's) vary, the simplest example being the generators of a quadric in S3. Another method of obtaining loci having these properties is by taking the flat spaces through the sets of a linear series of sets of points on an elliptic curve and the flat spaces through the sets of the residual series (the curve being supposed normal. In this way we shall obtain a configuration of ∞PSP's and ∞qSq's, the dual of which gives a locus included among those represented by (1).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 3 , 20 September 1924 , pp. 319 - 324
Copyright
Copyright © Cambridge Philosophical Society 1924

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Segre, C., Rend. Circ. Mat. Palermo, 5 (1891), p. 192.CrossRefGoogle Scholar
(2)Schur, F., Math. Annalen, 23 (1884), p. 437.CrossRefGoogle Scholar
(3)Study, E., Methoden…ternären Formen (Leipzig, 1889), p. 119.Google Scholar
(4)Segre, C., Math. Annalen, 40 (1892), p. 413.CrossRefGoogle Scholar
(5)Segre, C., Rend. Circ. Mat. Palermo, 30 (1910), p. 93.Google Scholar
(6)Duschek, A., Monatshefte f. Math. u. Physik (1923), p. 63. Also Encyk., p. 958, above cited.CrossRefGoogle Scholar
(1)Kantor, S., Sitzungsberichte Königl. Bayr. Akad. München, 27 (1897), p. 367.Google Scholar
(2)Kantor, S., Monatshefte f. Math. u. Physik, 11 (1900), p. 193.Google Scholar
See Encyk., pp. 927–932, above cited.Google Scholar
(1)Kötter, , Preisschrift (1887).Google Scholar
(2)Kantor, S., Journ. f. Math., 118 (1897), p. 74.Google Scholar
(3)Zindler, K., Journ. f. Math., 111 (1893), p. 303.Google Scholar
(4)Perazzo, U., Mem. Torino Accad. (2), 54 (1904), p. 149, also Encyk., p. 43, above cited.Google Scholar
(1)Segre, C., Math. Annalen, 27 (1886), p. 296.CrossRefGoogle Scholar
(2)Rosati, C., Rend. Ist. Lombardo (2), 35 (1902), p. 407.Google Scholar
(3)Veneroni, E., Rend. Ist. Lombardo (2), 38 (1905), p. 523.Google Scholar
(4)Marietta, G., Atti Accad. Gioenia di Catania (5), 1 (1908), also Encyk., p. 904, above cited.Google Scholar
(5)Veronese, G., Mem. Accad. Lincei (3), 19 (1884), p. 344.Google Scholar
(6)Perazzo, U., Accad. Sci. Torino, Atti, 36 (1901), p. 891.Google Scholar