Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T14:04:49.065Z Has data issue: false hasContentIssue false
  • English
  • Français

On lifting Fuchsian Groups

Published online by Cambridge University Press:  24 October 2008

A. H. M. Hoare
A. H. M. Hoare
Affiliation:
University of Birmingham
Get access Rights & Permissions [Opens in a new window]

Extract

Let Γ be a discrete subgroup of G = PSL(2,ℝ) and p be the canonical map from the universal covering group 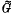on to PSL(2,ℝ). By a continuity argument on a fundamental polygon for Γ acting on the hyperbolic plane 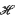2, Milnor (4) obtained a presentation for p−1(Γ) whenever 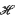2/Γ is compact and of genus zero. Using Teichmüller theory and a double Reidemeister-Schreier process, Macbeath(2) showed that the general compact case can be deduced from Milnor's result. We give here a method of obtaining a presentation which uses only the geometry of a Dirichlet region and which applies equally to the non-compact case.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 87 , Issue 1 , January 1980 , pp. 61 - 67
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hoare, A. H. M., Karrass, A. and Solitar, D.Subgroups of infinite index in Fuchsian groups. Math. Z. 125 (1972), 59–69.Google Scholar
(2)Macbeath, A. M. The fundamental groups of the three-dimensional Brieskorn manifolds. (Preprint.)Google Scholar
(3)Macbeath, A. M. and Hoare, A. H. M.Groups of hyperbolic crystallography, Math. Proc. Cambridge Philos. Soc. 79 (1976), 235–249.CrossRefGoogle Scholar
(4)Milnor, J. On the 3-dimensional Brieskorn Manifolds M(p, q, r). In Knots, groups and 3-manifolds (ed. Neuwirth, L. P.). Ann. of Math. Stud. 84 (1975).Google Scholar
(5)Pontrjagin, L.Topological groups (Princeton University Press, 1939).Google Scholar