Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Okikiolu, G. O.
1970.
On integral operators with kernels involving Bessel functions (Correction and Addendum).
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 67,
Issue. 3,
p.
583.
McBride, Adam C.
1975.
A Theory of Fractional Integration for Generalized Functions.
SIAM Journal on Mathematical Analysis,
Vol. 6,
Issue. 3,
p.
583.
McBride, Adam C.
1978.
The Hankel transform of some classes of generalized functions and connections with fractional integration.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 81,
Issue. 1-2,
p.
95.
Brychkov, Yu. A.
Glaeske, H. -J.
and
Marichev, O. I.
1985.
Factorization of integral transformations of convolution type.
Journal of Soviet Mathematics,
Vol. 30,
Issue. 3,
p.
2071.
Kilbas, A.A.
Saigo, M.
and
Trujillo, J.J.
2000.
On The Meijer Transform In Space.
Integral Transforms and Special Functions,
Vol. 10,
Issue. 3-4,
p.
267.
Gromak, Elena V.
and
Kilbas, Anatoly A.
2005.
Asymptotic expansions of 𝒴ηtransform.
Integral Transforms and Special Functions,
Vol. 16,
Issue. 5-6,
p.
407.



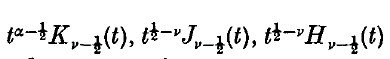 and
and 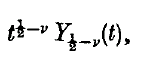 and in the last three cases the integrals converge in norm.
and in the last three cases the integrals converge in norm.