Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rajagopal, C. T.
1955.
A note on ingham summability and summability by Lambert series.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 42,
Issue. 1,
p.
41.
Segal, S. L.
1966.
On Ingham's Summation Method.
Canadian Journal of Mathematics,
Vol. 18,
Issue. ,
p.
97.
Segal, S. L.
1967.
Summability by Dirichlet convolutions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 63,
Issue. 2,
p.
393.
Jukes, K. A.
1969.
On the Dirichiet product of Cesàro-summable series.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 66,
Issue. 3,
p.
563.


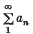 defined by
defined by