Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T14:17:26.811Z Has data issue: false hasContentIssue false
  • English
  • Français

On H-balls and canonical regions of loxodromic elements in complex hyperbolic space

Published online by Cambridge University Press:  24 October 2008

Shigeyasu Kamiya
Shigeyasu Kamiya
Affiliation:
Department of Mechanical Engineering, Okayama University of Science, 1-1 Ridai-cho Okayama 700, Japan Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, 16 Mill Lane, CambridgeCB2 1SB
Get access Rights & Permissions [Opens in a new window]

Extract

Let U(1, n; ℂ) be the automorphism group of the Hermitian form

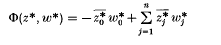
for 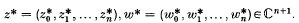. We can regard an element of U(1, n; ℂ) as a transformation acting on 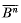, where 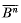is the closure of the complex unit ball

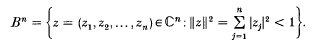
The non-trivial elements of U(1, n; ℂ) fall into three conjugacy types, depending on the number and the location of their fixed points. Let g be a non-trivial element of U(1, n; ℂ). We call g elliptic if it has a fixed point in Bn and g parabolic if it has exactly one fixed point and this lies on the boundary ∂Bn. An element g will be called loxodromic if it has exactly two fixed points and they lie on ∂Bn.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 113 , Issue 3 , May 1993 , pp. 573 - 582
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Beardon, A. F.. The Geometry of Discrete Groups. Graduate Texts in Math, no. 91 (Springer-Verlag, 1983).CrossRefGoogle Scholar
[2]Beardon, A. F. and Nicholls, P. J.. On classical series associated with Kleinian groups. J. London Math. Soc. (2) 5 (1972), 645–655.CrossRefGoogle Scholar
[3]Kamiya, S.. On some series associated with discrete subgroups of U( 1, n; ℂ). Math. J. Okayama Univ. 26 (1984), 193–197.Google Scholar
[4]Kamiya, S.. Discrete subgroups of U( 1, a; ℂ) on the product space ∂Bn × ∂Bn × … × ∂Bn. Quart. J. Math. Oxford (2) 41 (1990), 287–294.CrossRefGoogle Scholar
[5]Kamiya, S.. Discrete subgroups of convergence type of U(1, n; ℂ). Hiroshima Math. J. 21 (1991), 1–21.CrossRefGoogle Scholar
[6]Kamiya, S.. Notes on elements of U(1, n; ℂ). Hiroshima Math. J. 21 (1991), 23–45.Google Scholar
[7]Kamiya, S.. The action of discrete subgroups of U(1, n; ℂ) on ∂Bn. Math. Japon 37 (1992), 927–933.Google Scholar
[8]Patterson, S. J.. The limit set of a fuchsian group. Ph.D. thesis, University of Cambridge (1974).Google Scholar