Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-30T20:20:12.676Z Has data issue: false hasContentIssue false
  • English
  • Français

On Hausdorff's methods of summability. II

Published online by Cambridge University Press:  24 October 2008

W. W. Rogosinski
W. W. Rogosinski
Affiliation:
King's CollegeAberdeen
Get access Rights & Permissions [Opens in a new window]

Extract

A general theory of ‘strength’ for Hausdorff methods T of summability was given in the first part of this paper, to which we shall refer in the following as I. Those methods T which are regular (that is, at least as strong as ordinary convergence C), are defined by the linear transforms

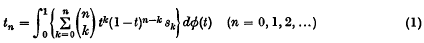
of a given sequence (sk). Here ø(t) (that is, each of its real and imaginary parts) is of bounded variation (b.v.) in the closed interval 〈0, 1〉 [see I, (4)]. The additional condition for consistency (with C) is that ø(t) is continuous at t = 0, and that ø(1) − ø(0) = 1 [I, H. 3]. We write also T ˜ ø(t).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 38 , Issue 4 , November 1942 , pp. 344 - 363
Copyright
Copyright © Cambridge Philosophical Society 1942

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hardy, G. H. and Riesz, M.The general theory of Dirichlet series (Cambridge, 1915).Google Scholar
(2)Hille, E. and Rasch, G.Über die Nullstellen der unvollständigen Gammafunktion. II. Math. Z. 29 (1929), 319–34.CrossRefGoogle Scholar
(3)Mercer, J.On the limits of real variants. Proc. London Math. Soc. (2), 5 (1907), 206–24.CrossRefGoogle Scholar
(4)Pitt, H. R.Mercerian Theorems. Proc. Cambridge Phil. Soc. 34 (1938), 510–20.CrossRefGoogle Scholar
(5)Rasch, G.Über die Nullstellen der unvollständigen Gammafunktion. I. Math. Z. 29 (1929), 300–18.CrossRefGoogle Scholar
(6)Riesz, M.Sur les séries de Dirichlet et les séries entières. C. R. Acad. Sci., Paris (1909).Google Scholar
(7)Rogosinski, W.Über die Abschnitte trigonometrischer Reihen. Math. Ann. 95 (1925), 110–34.CrossRefGoogle Scholar
(8)Rogosinski, W.Reihensummierung durch Abschnittskoppelungen. Math. Z. 25 (1926), 132–49.CrossRefGoogle Scholar
(9)Rogosinski, W.On Hausdorff's Methods of summability. Proc. Cambridge Phil. Soc. 38 (1942), 166–92.CrossRefGoogle Scholar
(10)Saks, S.Theory of the integral, 2nd ed. (Warsaw, 1937).Google Scholar
(11)Silverman, L. L.On the consistency and equivalence of certain generalized definitions of the limit of a function of a continuous variable. Ann. Math. 21 (1919), 128–40.CrossRefGoogle Scholar