Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-30T22:21:14.696Z Has data issue: false hasContentIssue false
  • English
  • Français

On functions of bounded variation†

Published online by Cambridge University Press:  26 July 2016

CHRISTOPH AISTLEITNER ,
FLORIAN PAUSINGER ,
ANNE MARIE SVANE  and
ROBERT F. TICHY
CHRISTOPH AISTLEITNER
Affiliation:
Johannes Kepler University Linz e-mail: [email protected]
FLORIAN PAUSINGER*
Affiliation:
TU Munich e-mail: [email protected]
ANNE MARIE SVANE
Affiliation:
Aarhus University e-mail: [email protected]
ROBERT F. TICHY
Affiliation:
TU Graz e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The recently introduced concept of 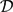${\mathcal D}$-variation unifies previous concepts of variation of multivariate functions. In this paper, we give an affirmative answer to the open question from [20] whether every function of bounded Hardy–Krause variation is Borel measurable and has bounded 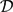${\mathcal D}$-variation. Moreover, we show that the space of functions of bounded 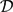${\mathcal D}$-variation can be turned into a commutative Banach algebra.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 162 , Issue 3 , May 2017 , pp. 405 - 418
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Corresponding author: Florian Pausinger, TU Munich, Zentrum Mathematik, M10 Geometrie und Visualisierung, Boltzmannstr. 3, 85748 Garching.

References

REFERENCES

[1] Adams, C. R. and Clarkson, J. A. Properties of functions f(x, y) of bounded variation. Trans. Amer. Math. Soc. 36 (1934), 711–730.Google Scholar
[2] Aistleitner, C. and Dick, J. Functions of bounded variation, signed measures and a general Koksma–Hlawka inequality. Acta Arith 167 (2015), 143–171.CrossRefGoogle Scholar
[3] Antosik, P. Study of the continuity of a function of many variables (Russian). Prace Mat. 10 (1966), 101–104.Google Scholar
[4] Blümlinger, M. and Tichy, R. F. Topological Algebras of Functions of Bounded Variation I. Manuscripta Math. 65 (1989), 245–255.CrossRefGoogle Scholar
[5] Blümlinger, M. Topological Algebras of Functions of Bounded Variation II. Manuscripta Math. 65 (1989), 377–384.CrossRefGoogle Scholar
[6] Brandolini, L., Colzani, L., Gigante, G. and Travaglini, G. On the Koksma–Hlawka inequality. J. Complexity 29 (2013), 158–172.CrossRefGoogle Scholar
[7] Brandolini, L., Colzani, L., Gigante, G. and Travaglini, G. A Koksma–Hlawka inequality for simplices, Trends in Harmonic Analysis. Springer INdAM Ser. 3 (Springer, Milan, 2013), 33–46.CrossRefGoogle Scholar
[8] Clarkson, J. A. and Adams, C. R. On definitions of bounded variation for functions of two variables. Trans. Amer. Math. Soc. 35 (1933), 824–854.CrossRefGoogle Scholar
[9] Drmota, M. and Tichy, R. F. Sequences, discrepancies and applications. Lecture Notes in Mathematics (Springer-Verlag, Berlin, 1997), 1651.CrossRefGoogle Scholar
[10] Götz, M. Discrepancy and the error in integration. Monatsh. Math. 136 (2002), no. 2, 99–121.Google Scholar
[11] Hardy, G. H. On double Fourier series, and especially those which represent the double zeta-function with real and incommensurable parameters. Quart. J. Math. (1) 37 (1906), 53–79.Google Scholar
[12] Harman, G. Variations on the Koksma–Hlawka inequality. Unif. Distrib. Theory 5 (2010), 65–78.Google Scholar
[13] Hlawka, E. Funktionen von beschränkter Variation in der Theorie der Gleichverteilung. Ann. Math. Pura Appl. 54 (1961), 325–333.CrossRefGoogle Scholar
[14] Idczak, D. Functions of several variables of finite variation and their differentiability. Ann. Polon. Math. 60 (1994), no. 1, 47–56.CrossRefGoogle Scholar
[15] Koksma, J. F. A general theorem from the theory of uniform distribution modulo 1. Mathematica B (Zutphen) 11 (1942), 7–11.Google Scholar
[16] Krause, J. M. Fouriersche Reihen mit zwei veränderlichen Grössen. Ber. Sächs. Akad. Wiss. Leipzig 55 (1903) 164–197.Google Scholar
[17] Kuipers, L. and Niederreiter, H. Uniform Distribution of Sequences (Wiley-Interscience John Wiley & Sons, New York–London–Sydney, 1974).Google Scholar
[18] Leonov, A. S. Remarks on the total variation of functions of several variables and on a multidimensional analogue of Helly's choice principle. (in Russian) Mat. Zametki 63 (1998), 69–80.Google Scholar
[19] Owen, A. B. Multidimensional variation for quasi-Monte Carlo. Contemporary multivariate analysis and design of experiments. Ser. Biostat. 2 (World Scientific Publishing Co. Pte. Ltd., 2005), 49–74.Google Scholar
[20] Pausinger, F. and Svane, A. M. A Koksma–Hlawka inequality for general discrepancy systems. J. Complexity 31 (2015), 773–797.CrossRefGoogle Scholar
[21] Yeh, J. Real analysis. Theory of measure and integration. Second edition (World Scientific Publishing Co. Pte. Ltd., 2006).CrossRefGoogle Scholar
[22] Young, W. H. and Young, G. On the discontinuties of monotone functions of several variables. Proc. London Math. Soc. (2) 22 (1923), 124–142.Google Scholar