Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T14:53:58.515Z Has data issue: false hasContentIssue false
  • English
  • Français

On functional Nörlund methods

Published online by Cambridge University Press:  24 October 2008

B. Choudhary
B. Choudhary
Affiliation:
I.I.T. Delhi, Haus-Khas, New Delhi 29, India
Get access Rights & Permissions [Opens in a new window]

Extract

Integral transformations analogous to the Nörlund means have been introduced and investigated by Kuttner, Knopp and Vanderburg(6), (5), (4). It is known that with any regular Nörlund mean (N, p) there is associated a function

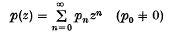
regular for |z| < 1, and if we have two Nörlund means (N, p) and (N, r), where (N, pr is regular, while the function 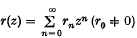is regular for |z| ≤ 1 and different) from zero at z = 1, then q(z) = r(z)p(z) belongs to a regular Nörlund mean (N, q). Concerning Nörlund means Peyerimhoff(7) and Miesner (3) have recently obtained the relation between the convergence fields of the Nörlund means (N, p) and (N, r) on the one hand and the convergence field of the Nörlund mean (N, q) on the other hand.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 1 , January 1970 , pp. 47 - 60
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Doetsch, G.Theorie und Anwendung der Laplace-Transformation (Berlin, 1937).CrossRefGoogle Scholar
(2)Hardy, G. H.Divergent series (Oxford, 1949).Google Scholar
(3)Miesner, W.The convergence fields of Nörlund means. Proc. London Math. Soc.. 3 (1965), 495–507.CrossRefGoogle Scholar
(4)Knopp, K.Nörlund-Verfahren für functionen. Math. Z.. 63 (1955), 39–52.CrossRefGoogle Scholar
(5)Knopp, K. and Vanderburg, B.Functional Nörlund Methods. I. Rend. Circ. Mat. Palermo. (1955), 5–32.CrossRefGoogle Scholar
(6)Kuttner, B.The generalized limit of a function. Proc. London Math. Soc.. 2 (1941), 142–173.Google Scholar
(7)Peyerimhoff, A.On convergence fields of Nörlund means. Proc. Amer. Math. Soc.. (1956), 335–347.Google Scholar
(8)Titchmarsh, E.Introduction to the theory of Fourier Integrals (Oxford 1937).Google Scholar
(9)Widder, D. V.The Laplace transform (Princeton, 1941).Google Scholar
(10)Wiener, N. and Pitt, H. R.On absolutely convergent Fourier-Stieltjes transforms. Duke Math. J. 4 (1938), 420–436.CrossRefGoogle Scholar