Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T19:01:04.696Z Has data issue: false hasContentIssue false
  • English
  • Français

On filling families of finite subsets of the Cantor set

Published online by Cambridge University Press:  01 July 2008

PANDELIS DODOS  and
VASSILIS KANELLOPOULOS
PANDELIS DODOS
Affiliation:
National Technical University of Athens, Faculty of Applied Sciences, Department of Mathematics, Zografou Campus, 157 80, Athens, Greece. e-mail: [email protected], [email protected]
VASSILIS KANELLOPOULOS
Affiliation:
National Technical University of Athens, Faculty of Applied Sciences, Department of Mathematics, Zografou Campus, 157 80, Athens, Greece. e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

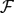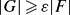Let ϵ > 0 and be a family of finite subsets of the Cantor set . Following D.H. Fremlin, we say that is ϵ-filling over if is hereditary and for every F ⊆ finite there exists G ⊆ F such that G ϵ and . We show that if 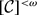is ϵ-filling over and C-measurable in , then for every 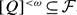P ⊆ perfect there exists Q ⊆ P perfect with . A similar result for weaker versions of density is also obtained.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 145 , Issue 1 , July 2008 , pp. 165 - 175
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Apter, A. W. and Džamonja, M.. Some remarks on a question of D.H. Fremlin regarding ϵ-density, Arch. Math. Logic 40 (2001), 531–540.CrossRefGoogle Scholar
[2]Argyros, S. A. and Todorčević, S.. Ramsey methods in analysis. Advanced Courses in Mathematics, CRM Barcelona (Birkhäuser Verlag, 2005).CrossRefGoogle Scholar
[3]Becker, H. and Kechris, A. S.. The descriptive set theory of polish group actions. London Math. Soc. Lecture Note Series 232 (Cambridge University Press, 1996).CrossRefGoogle Scholar
[4]Blass, A.. A partition theorem for perfect sets. Proc. Amer. Math. Soc. 82 (1981), 271–277.CrossRefGoogle Scholar
[5]Erdös, P. and Magidor, M.. A note on regular methods of summability and the Banach-Saks property. Proc. Amer. Math. Soc. 59 (1976), 232–234.CrossRefGoogle Scholar
[6]Fremlin, D. H.. Problem DU available at www.essex.ac.uk/maths/staff/fremlin/problems.htm.Google Scholar
[7]Kechris, A. S.. Classical descriptive set theory, Grad. Texts in Math. 156 (Springer-Verlag, 1995).CrossRefGoogle Scholar
[8]Louveau, A., Shelah, S. and Veličković, B.. Borel partitions of infinite subtrees of a perfect tree. Annals Pure Appl. Logic 63 (1993), 271–281.Google Scholar
[9]Solovay, R. M.. A model of set theory in which every set of reals is Lebesgue measurable. Annals of Math. 92 (1970), 1–56.Google Scholar