Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T14:56:47.354Z Has data issue: false hasContentIssue false
  • English
  • Français

On complex vector bundles on rational threefolds

Published online by Cambridge University Press:  24 October 2008

Constantin BẮnicẮ  and
Mihai Putinar
Constantin BẮnicẮ
Affiliation:
Department of Mathematics, Increst, Bucharest, Romania
Mihai Putinar
Affiliation:
Department of Mathematics, Increst, Bucharest, Romania
Get access Rights & Permissions [Opens in a new window]

Extract

It is known [14] that every topological complex vector bundle on a smooth rational surface admits an algebraic structure. In [10] one constructs algebraic vector bundles of rank 2 on 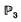with arbitrary Chern classes c1, c2 subject to the necessary topological condition c1 c2 = 0 (mod 2). However, in dimensions greater than 2 the Chern classes don't determine the topological type of a vector bundle. In [2] one classifies the topological complex vector bundles of rank 2 on 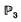and one proves that any such bundle admits an algebraic structure.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 97 , Issue 2 , March 1985 , pp. 279 - 288
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atiyah, M. F. and Hirzebruch, F.. Vector bundles and homogeneous spaces. Proceedings of Symposia of A.M.S., vol. III (1960), 20–104.Google Scholar
[2]Atiyah, M. F. and Rees, E.. Vector bundles on projective 3-spaces. Invent. Math. 35 (1976), 131–153.CrossRefGoogle Scholar
[3]BẮnicẮ, C.. Topologisch triviale holomorphe Vektorbündel auf ℙn(ℂ). J. reine angew. Math. 344 (1983), 102–119.Google Scholar
[4]BẮnicẮ, C. and Forster, O.. Sur les structures multiples (manuscrit).Google Scholar
[5]Ferrand, D.. Courbes gauches et fibres de rang 2. C. R. Acad. Sci. Paris, 281 (1975), 345–347.Google Scholar
[6]Griffiths, P. A. and Adams, J.. Topics in algebraic and analytic geometry (Princeton University Press, 1974).Google Scholar
[7]Hartshorne, R.. Algebraic geometry (Springer-Verlag, 1977).CrossRefGoogle Scholar
[8]Hartshorne, R.. Stable vector bundles of rank 2 on ℙ3. Math. Ann. 238 (1978), 229–280.CrossRefGoogle Scholar
[9]Hirzebruch, F.. Topological methods in algebraic geometry. (Springer-Verlag, 1966).Google Scholar
[10]Horrocks, G.. A construction for locally free sheaves. Topology 7 (1968), 117–120.CrossRefGoogle Scholar
[11]Husemoller, D.. Fibre bundles (McGraw-Hill, 1966).CrossRefGoogle Scholar
[12]Okonek, C., Schneider, M. and Spindler, H.. Vector bundles on complex projective spaces. (Birkhäuser, 1980).Google Scholar
[13]Peterson, F. P.. Some remarks on Chern classes. Ann. of Math. 69 (1959), 414–420.CrossRefGoogle Scholar
[14]Schwabzenberger, R. L. E.. Vector bundles on algebraic surfaces. Proc. London Math. Soc. 11 (1961), 601–622.CrossRefGoogle Scholar
[15]Switzer, R. M.. Postnikov towers associated with complex 2-plane and symplectic line bundles. Math. Z. 168 (1979), 87–103.CrossRefGoogle Scholar