Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T13:13:34.876Z Has data issue: false hasContentIssue false
  • English
  • Français

On certain nets of plane curves

Published online by Cambridge University Press:  24 October 2008

F. P. White
F. P. White
Affiliation:
St John's College
Get access Rights & Permissions [Opens in a new window]

Extract

1. The plane quartic curves which pass through twelve fixed points g, of which no three lie on a straight line, no six on a conic and no ten on a cubic, form a net of quartics represented by the equation

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 1 , February 1924 , pp. 1 - 10
Copyright
Copyright © Cambridge Philosophical Society 1924

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

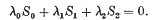
* See Küpper, C., “Über geometrische Netze” [Abh. d. k. bōhm. Gesell. d. Wiss., Prag, (7) I (1886)].Google Scholar The existence of such nets affords an example of the exceptions pointed out by Bacharach, [Math. Ann. XXVI (1886), 275]CrossRefGoogle Scholar to a theorem of Cayley's [Papers, I, 25] that a curve of order p=m+n-γ passing through

of the points of intersection of two curves of orders m and n passes also through the remaining

. This no longer holds if these

points lie on a curve of order γ -3. In our case m=n=γ=4. This example has been given for many years by Mr Richmond in his lectures on Plane Algebraic Geometry at Cambridge.

† See White, F. P., Proc. Camb. Phil. Soc. XXI (1922), 216.Google Scholar

* Projecting from P on to a hyperplane, we get a quintic surface in ordinary space with a double twisted cubic curve; this surface was investigated years ago by Clebsch, [Math. Ann. 1 (1869), 284]Google Scholar; the hyperelliptic curve is the representation of the double curve.